225. THE GENEALOGIES OF SCALES AFTER THE ANCIENT GREEK MUSICAL SYSTEM
In ancient Greece according to Aristoxenos, and Euclid's katatomi kanonos, there were 3 musical gendres , the diatonic , the chromatic and enharmonic which were also tetrachords (total length an interval of 4th) and pentachords (total legth an interval of 5th and consisting from an initial or final tone and a tetrachord as before) and by combing a tetrachord with a pentachord they got various 7-notes scales inside an octave . In other words the 7-notes scale was of the form Tetrachord1+2+tetrachord2 , in which case it was called two "divorced" tercahords or Tetrachord1+tetrachord2+2 in which case it was called two adjoint tetrachords. 1) the Diatonic was balanced feelings (that eventually after more than 1 thousand years resulted to the 7-notes diatonic scale, and a simplified rounding of their tetrcahords to a single one was the 2-2-1 and most probably all permutations of it ) the 2) Chromatic was sad feelings (that eventually after more than 1 thousand years resulted to the 7-notes harmonic minor and double harmonic minor scales, blues scale etc , And a simplified rounding of their tetrachords to a single one was the 3-1-1 nd most probably all permutations of it ) and 3) the enharmonic was happy feelings (used major 3rd intervals and a simplified rounding to a single one was the 4-(1/2)-(1/2)) and most probably all permutations of it ) and has many similarities with the Japanese 5-notes scales like the Akebono with interval structure 4 - 2 - 1 - 4 - 1 e.g. at the mode 2-1-4-1-4 e.g. A B C E F A. (See e.g. the video https://www.youtube.com/watch?v=vv7CO-nVFj8 )
THE RESRICTED ENUMERATION-GENERATION OF SCALES ACCORDING TO EUCLID'S KATATOMH KANONOS OF ANCIENT GREEK MUSICAL SYSTEM
This is based on the next restrictions
1) Smaller intervals in a tetrachord are always at lower frequencies
2) When joining two tetrachords either we put an inteval of one tone in betwenn, or at the end of the 2nd tetrachord
In ancient Greece according to Aristoxenus the tetrachords where 6 and of 3 gendres
They divided the semitone in to 6 equal segments, or the octave in to 72 segments or the pure 4th in to 30 segments.
Then the tetrachords were the next (the integers are Aristoxenus segments, the fractions of a tone by Euclid in Katatomh kanonos))
ENHARMONIC GENDRE
3-3-24 or semitone/2 -- semitone/2 --2 tones
CHROMATIC GENDRE
Soft 4-4-22 or 1/3 tone 1/3 tone 11/6 of a tone
hemiolion 4.5 -4.5 -21 or 3/8 tone 3/8 tone and 7/4 of a tone
tonal 6-6-18 or 1 semitone 1 semitone 3 semitones
DIATONIC GENDRE
uniform soft 6-9-15 or 1/2 tone 3/4 tone and 5/4 tone
syntono strong 6-12-12 or 1/2 tone , 1 tone 1 tone
Now two tetrachords make a scale of an octave in two ways
The disjunctive way = tetrachord+1tone+tetrachord=5+2+5 semitones=12 semitones
Or the adjoint way = tetrachord+tetrachord+1 tone=5+5+2 semitones=12 semitones
E.g. syntono+1tone+syntono=diatonic scale lydian mode
or syntono+syntono+1tone=diatonic scale Locrian mode
or tonal+tonal+1tone=6-6-18-6-6-18-12 which is a mode ofthe by now known as inverse persian todi theta scale
The same with the tonal+1tone+tonal.
etc
See also post 227
For reasons of completeness we enumerate here the trichords which are of length an interval of 3rd.
All of them are of the DIATONIC FAMILY
1-2
2-1
2-2
CHROMATIC GENDREThey divided the semitone in to 6 equal segments, or the octave in to 72 segments or the pure 4th in to 30 segments.
Then the tetrachords were the next (the integers are Aristoxenus segments, the fractions of a tone by Euclid in Katatomh kanonos))
ENHARMONIC GENDRE
3-3-24 or semitone/2 -- semitone/2 --2 tones
CHROMATIC GENDRE
Soft 4-4-22 or 1/3 tone 1/3 tone 11/6 of a tone
hemiolion 4.5 -4.5 -21 or 3/8 tone 3/8 tone and 7/4 of a tone
tonal 6-6-18 or 1 semitone 1 semitone 3 semitones
DIATONIC GENDRE
uniform soft 6-9-15 or 1/2 tone 3/4 tone and 5/4 tone
syntono strong 6-12-12 or 1/2 tone , 1 tone 1 tone
Now two tetrachords make a scale of an octave in two ways
The disjunctive way = tetrachord+1tone+tetrachord=5+2+5 semitones=12 semitones
Or the adjoint way = tetrachord+tetrachord+1 tone=5+5+2 semitones=12 semitones
E.g. syntono+1tone+syntono=diatonic scale lydian mode
or syntono+syntono+1tone=diatonic scale Locrian mode
or tonal+tonal+1tone=6-6-18-6-6-18-12 which is a mode ofthe by now known as inverse persian todi theta scale
The same with the tonal+1tone+tonal.
etc
See also post 227
For reasons of completeness we enumerate here the trichords which are of length an interval of 3rd.
All of them are of the DIATONIC FAMILY
1-2
2-1
2-2
Because half semitones are not palyable in he piano, and we want to enumarate scales and sbscales of the ancient Greek system playable in the piano, we simplyfy the tetrachords to the next
ENHARMONIC GENDRE
1-4 semitones, inteeval of 4th
1-4 semitones, inteeval of 4th
1-1-3 semitones
DIATONIC GENDRE
1- 2-2 semitones
1- 2-2 semitones
Then we start combining tetrachords to obtain scales of one octave.
We can combine a gendre with itself (pure gendre) or a gendre with another gendre to obtain an hybrid gendres.
E.g. all 3*3=9 cases are
1) Diatonic-Diatonic
2) Chromatic -chromatic (double chormatic)
3) Enharmonic-enharmonic (double enharmonic)
4) Diatonic-Chromatic
5) Chromatic-Diatonic
6) Diatonic-enharmonic
7) Enharmonic-diatonic
8) Chromatic-enharmonic
9) Enharmonic-chromatic
To this we may add the possibility that the combination is diazeuksis (one tone in between) , or syzeuksis (a tone at the end) , In principle we get 18 combinations but some of them give the same scale.
Let us look in detail to the scales.
1) Diatonic-Diatonic gives
1-2-2-2-1-2-2 (diazeyksis) or 1-2-2-1-2-2-2 (syzeyksis) which is again the well known 7-notes diatonic scale.
2) Chromatic -chromatic (double chormatic) gives
1-1-3-2-1-1-3 (diazeuksis) and 1-1-3-1-1-3-2 (syzeyksis) which is aagain the same scale (but different modes) which is the parachromatic scale, or the blues scale with a leading tone. It is called also inverse persian scale and Purvi theta scale.
3) Enharmonic-enharmonic (double enharmonic) gives
The pentatonic scale
1-4-2-1-4 (diazeuksis) and 1-4-1-4-2 (syzeuksis) both are the same pentatonic scale. It is called Lydian pentatonic and it is also met in japan and is also called Hirajoshi scale. The japanese santuri, called Koto, is tuned in it. It is met also in India as Raga Amritavarshini, Malashri, Shilangi, and in Ethiopia as Batti Lydian (See post 227)
4) Diatonic-Chromatic gives
1-2-2-2-1-1-3 (by diazeyksis) or 1-2-2-1-1-3-2 (by syzeuksis), that are different scales!
The 1-2-2-2-1-1-3 is called sabach .
For the sabach see
It is also met in India under the name Mela Senavati (see post 227)
The 1-2-2-1-1-3-2 may be called dual of sabach, as it is also obtained as
Cromatic-Diatonic instead of Diatonic-Chromatic .
The Neapolitan minor is the inverse of the sabach scale . See
The 6) Diatonic-enharmonic gives
1-2-2-2-1-4 , which is a hexatonic scale , met at least in india under the name Mela Suddha Simantini (see post 227) . It has the 2 chords 4M 3 m . It is also met as in Cretan folk melodies in Lyra. It is related also (it contains as subsale) to the pentatonic scale Akebono.
The 7) Enharmonic-Diatonic gives
the hexatonic scale 1-2-2-1-4-2 , which is met in japan as Honchchi plagal form (see post 227)
and is also a hexatonic version of the diatonic Locrian mode.
Finally the
The 8) Chromatic-enharmonic gives the hexatonic
1-1-3-2-1-4, which is met in India as inverse Raga Tilang.
The 9) Enharmonic-chromatic gives the hexatonic
1-4-2-1-1-3 , which is met in India as raga kalakhanthi
The alternatives diazeuksi or syzeyksi again lead the same scales.
THE 1ST FREE GENERATION OF SCALES AND MODES AFTER THE ANCIENT GREEK MUSICAL SYSTEM.
This is based on the next rules
1) Any order of the intervals in semitones in a tetrachord. We allow permutations of the intervals of the ancient Greek tetrachords in all the 3 gendres
2) Any comination of a tetrachord and a pentachord.
3) We retain the 1/2 semitone intervals in the 1st desgn but then we simpolify two consecutive of them to an interval of semitone so as the scale finally si playable in the piano.
In Ancient Greece, Byzantine and middle east, the 7-notes scales were created by combining 4-notes (tetrachords) that have total length an interval of 4th and 5-notes (pentachords) that have total length and interval of 7th. In this way all such 7-notes scales contain the power-5 chord 1-5-1' (e.g. C3-G3-C4).
The representation of such tetrachords and pentachords can be with the sequence of intervals in semitones. Thus to find all of them is in mathematical terminology to find all partitions of 5 in ti 3 numbers (having sum 5) and all partitions of 7 in to 4 numbers (having sum 7).
The solutions is the next
ALL 6 TETRACHORDS
DIATONIC GENDRE (FAMILY)
(containing only 2 and 1)
2-2-1 syntono major , Ionian/mixolydian (known also as Rast/Tsargiak/Mahour)
1-2-2 syntono minor , Phrygian/Locrian (known also as Qurdi)
2-1-2 minor, Dorian/Aeolian (known also as Bousselik/Nichavent/Ousak)
CHROMATIC GENDRE (FAMILY)
(containing 3)
1-3-1 2nd chromatic (known also as Hijaz)
1-1-3 parachromatic tonal
3-1-1 1st chromatic
ENHARMONIC GENDRE (FAMILY)
1/2-1/2-4
1/2-4-1/2
4-1/2-1/2
ENHARMONIC GENDRE (FAMILY)
1/2-1/2-4
1/2-4-1/2
4-1/2-1/2
All pentachords contain a single power-5 chord that power-5 chord which is defined by the end-notes of the pentachord.
THE DIATONIC FAMILY
(containing only 2, and 1)
2-2-2-1 Major Lydian Contains a major chord (known also as Natzi/Zaouil)
2-2-1-2 Major Ionian/Mixolydian Contains a major chord.(known also as Rast/Mahour)
2-1-2-2 Minor Dorian Contains a minor chord (known also as Bousselik/Nichavent)
1-2-2-2 Minor Frygian/Aeolian Contains a minor chord (known also as Qourdi)
THE CHROMATIC FAMILY
(containing 3 )
1-1-3-2
1-1-2-3
1-3-2-1 Contains a major chord and a diminished chord
1-2-3-1 Contains a minor chord and a diminished chord
1-2-1-3 Contains a minor chord and a diminished chord
1-3-1-2 Contains a major chord and a diminished chord (known also as Hijaz)
3-2-1-1 Contains a diminished chord
2-3-1-1
3-1-2-1 Contains a major chord and a diminished chord
2-1-3-1 Contains a minor chord and a diminished chord (known also as Nevesser/Nikriz)
3-1-1-2 Contains a major chord (known also as Saz-kar)
2-1-1-3 Contains a minor chord (known also as Samba)
THE ENHARMONIAN GENDRE (FAMILY)
(containing 4 )
1-1-1-4 Contains a minor chord
1-1-4-1
1-4-1-1
4-1-1-1 Contains a major chord
By combining a treachord and a pentachord we get a 7-notes scale. We remind the reader that in this book by scale we mean a sequence of notes giving an octave and all cyclic permutations of them are considered the same scale but also 7 different modes of it.
As a rough estimation of an upper bound on the number of the scales of this genealogy we calculate that if x is the number of different such scales then x<=6*20*2*2=480, because we will combine 6 tetrachords with 18 pentachords thus 6*20=120 such combinations, but also combining first 18 pentachords and then 6 tetrachords will give twice as many, thus 6*2*20=240 . And by taking also the inverse order on all notes of them at most 6*20*2*2=480 scales. Of course some of them will turn out to be simply modes (cyclic permutations ) of some previous or next, thus 480 is an upper bound not an exact number.
In this way we can get the next scale
1) The diatonic
2) The harmonic minor
3) The inverse of the harmonic minor
4) The Neopolitan minor scale
5) The inverse of the Neopolitan minor scale
6) The double harmonic minor
7) The melodic minor
8) The double melodic minor or Arabic scale or Neopolitan major
9) Parachromatic Byzantine scale (1-1-3-2-1-1-3)
10) Inverse parachromatic Byzantine
11) Debussy's 7-tonic (2-1-1-1-1-3-3) .
etc
Modes of the above 1-8 scales include the Byzantines minor and Byzantine double minor , Hungarian minor, Gypsy major and minor, Rast scale, Nikriz scale, Hitzaz scale, Hitzaskar scale , Nihavent scale, Neveser scale, 7-notes Sambach scale, Ousak scale , Qurdi scale , kartzigiar scale etc
Some japanese folk scales
Also arabic scales (projected in the Bach equally temperament 12-notes chromatic scale ) under the names Shouzinak , Housam, Shegiach , Moustaar , Persian or todi theta scale, the Enigmatic scale,
Debussy's 7-tonic (2-1-1-1-1-3-3) etc
etc
See also post 21.
And many more beautiful scales that are not known with any name!
I
OF SCPECIAL INTEREST IS THE 7-NOTE SCALE 2-2-1-2-1-2-2 E.G. C-D-E-F-G-G#-Bb-C WHICH IS DERIVED FROM THE FIRST 13 OVERTONES HARMONIC SERIES IN A NATURAL TRUMPET. AND IT IS CONSTRUCTED FROM THE 4-CHORD 2-2-1 AND THE 5-CHORD 2-1-2-2. IT IS THE MELODIC MINOR OR ACOUSTIC OVERTONES SCALE IF THE 7NTH HARMONIC E.G. IN C-D-E-F-G-G#-B-C if we interprete the 7nth overtone as B rather than Bb. BUT It is the inverse 7-notes scale of the first 13 overtones e.g. in a string or natural trumpet C-D-E-F-G-G#-B-C if we perceive THE 7NTH HARMONIC AS B
ALL 7-NOTES SCALES OF THE ENHARMONIC GENDRE BY COMBINING A DIATONIC TETRACHORD WITH AN ENHARMONIC PENTACHORD
2-2-1-1-1-1-4
2-2-1-4-1-1-1
2-2-1-1-4-1-1
2-2-1-1-1-4-1
1-2-2-1-1-1-4
1-2-2-4-1-1-1
1-2-2-1-4-1-1
1-2-2-1-1-4-1
2-1-2-1-1-1-4
2-1-2-4-1-1-1
2-1-2-1-4-1-1
2-1-2-1-1-4-1
ALL 6-NOTES (ENHARMONIC GENDER) SCALES THAT CONTAIN THE POWER-5 CHORD AND AT LEAST ONE MAJOR 3RD INTERVAL
Many of the irish melodies belong to such scales!
Because the power chord is contained, then there must exist an interval of 4th and an interval of 5th. If the interval of 4th contains a major 3rd then the only solutions are
4-1, 1-4 . Otherwise the interval of major 3rd must be contained inside the interval of 5th, and thus we have the 5-chords of the enharmonic gender
1-1-1-4 Contains a minor chord
1-1-4-1
1-4-1-1
4-1-1-1 Contains a major chord
In total we enumerate at first all such scales with 2 major 3rd intervals
1) 4-1-1-1-1-4
2) 1-4-1-1-1-4
3) 1-1-4-1-1-4
If there is only one major 3rd interval (4 semitones)
Then we combine the 1-4 , 4-1 with any 5-chord in the diatonic or chromatic gender
4) 1-4-2-2-2-1
5) 1-4-2-2-1-2
6) 1-4-2-1-2-2
7) 1-4-1-2-2-2
8) 1-4-1-1-3-2
9) 1-4-1-3-2-1
10) 1-4-1-2-3-1
11) 1-4-1-2-1-3
12) 1-4-1-3-1-2
13) 1-4-2-3-1-1
14) 1-4-3-1-2-1
15) 1-4-2-1-3-1
16) 1-4-3-1-1-2
17) 1-4-2-1-1-3
18) 4-1-2-2-1-2
19) 4-1-2-1-2-2
20) 4-1-1-2-2-2
21) 4-1-1-1-3-2
22) 4-1-1-2-3-1
23) 4-1-1-2-1-3
24) 4-1-3-1-1-2
25) 4-1-2-1-1-3
Among these 25 scales we filter the combinationof diatonic 4-chords and only one major third
thus haveing the 7 diatonic-enharmonic hexatonic scales
I have seydel harmonicas with these dtaitonic-enharmonic hexatonic scales
4) 1-4-2-2-2-1 (HEX ARABIC OR HEX NEAPOLITAN MAJOR 1M =inverse of 20) )
5) 1-4-2-2-1-2 (HEX MELODIC MINOR 1M-2d inverse of 19))
6) 1-4-2-1-2-2 (HEX DIATONICENHARMONIC 1m-2d)
7) 1-4-1-2-2-2 (HEX AKEBONO-CRETAN 1M-7m)
18) 4-1-2-2-1-2 (HEX ENHARMONIC 1M-7d)
19) 4-1-2-1-2-2 (HEX HMIN ENHARM 1m-7d inverse of 5) )
20) 4-1-1-2-2-2 (HEX ARABIC OR HEX NEAPOLITAN MAJOR 1m)
Among these 25 scales we filter those that contain the 4-3, or 3-4 which is triad chord as with more harmonic sound
Major chord 4-3:
14) 1-4-3-1-2-1
16) 1-4-3-1-1-2
By cyclic permutation we may re-write them as
14) 4-3-1-2-1-1
16) 4-3-1-1-2-1
16) 4-3-1-1-2-1
Minor chord 3-4:
23) 4-1-1-2-1-3
25) 4-1-2-1-1-3
By cyclic permutation we may re-write them as
23) 3-4-1-1-2-1
25) 3-4-1-2-1-1
ALL 5-NOTES SCALES THAT CONTAIN THE POWER-5 CHORD AND AT LEAST ONE MAJOR 3RD (4 SEMITONES)
This already mean that we know tow notes of the scale . The other 3
1) All in the lower interval of 5th . Thus a 5-chord as above and then an interval of 4th or 5 semitones.
1) 1-1-1-4 -5
2) 1-1-4-1-5
3) 1-4-1-1-5
4) 4-1-1-1 -5
2) All in the upper interval of 4th . Thus a 4-chord as above as as upper 3 notes and as lower notes the 3-4, 4-3 E.g.
5) 4-3-2-2-1 Known in this blog as the inverse maximal harmonic 5-tonic scale (see post 117 and 204 )
6) 4-3-1-2-2
7) 4-3-2-1-2
8) 4-3-1-3-1
9) 4-3-1-1-3
10) 4-3-3-1-1
and
11) 3-4-2-2-1
6) 3-4-1-2-2
7) 3-4-2-1-2
8) 3-4-1-3-1
9) 3-4-1-1-3
10) 3-4-3-1-1
3) 2 notes in the lower interval of 5th
3-2-2, 2-2-3, 4-2-1, 4-1-2 , 2-1-4, 1-2-4, 3-3-1, 1-3-3, 3-1-3, 1-1-5, 5-1-1, 1-5-1
and one in the upper interval of 4th
2-3, 3-2, 1-4 , 4-1 Thus
11) 3-2-2-4-1
12) 3-2-2-1-4
13) 2-2-3-1-4
14) 2-2-3-4-1 Known also as Greek pentatonic 2-2-3-4-1 (known also as Raga Chitthakarshini)
15) 4-2-1-2-3
16) 4-2-1-3-2
17) 4-2-1-1-4
18) 4-2-1-4-1 known also as the Japanese Hirajoshi 5-notes scale and In 5-notes scale and Iwato 5-notes scale and as Akebono 5-notes scale
19) 4-1-2-3-2
20) 4-1-2-1-4
21) 4-1-2-4-1
22) 2-1-4-2-3 known also as the Japanese Insen 5-notes scale
23) 1-2-4-2-3
24) 1-2-4-3-2
25) 1-2-4-4-1
26) 3-3-1-1-4
27) 3-3-1-4-1
28) 1-3-3-4-1
29) 3-1-3-1-4
30) 3-1-3-4-1
31) 1-1-5-1-4
32) 1-1-5-4-1
33) 5-1-1-1-4
34) 5-1-1-4-1
35) 1-5-1-4-1
36) 1-5-1-1-4
4) 1 note in the lower interval of 5th and 2 notes in the upper interval of 4th
thus 1-6, 6-1 and 1-1-1-2, 1-1-2-1, 1-2-1-1, 2-1-1-1, but none contains 4 , thus no new 5-notes scales.
2-1-4-1-4
THE 2ND FREE GENERATION OF SCALES AND MODES AFTER THE ANCIENT GREEK MUSICAL SYSTEM
This is based on the same rules as with the 1st free enumaration except
1) We do not need to obtain an octave scale, only by combining a tetrachord (interval of 4th) and a pentachord (interval of 5th) .
2) We stil keep the 3 geentres as
a) Pure diatonic gendre= Only intervals of 2nds
b) Pure Chromatic gendre=only intervals of 2nd and mior 3rd
c) Pure Enharmonic gendre=only intervals of 2nds and major thirds.
ALL THE 7 NOTE SCALES MADE ONLY FROM TONES AND SEMITONES
As it is known the diatonic scale (major or minor mode) is made from successive steps of one tone or one semitone. In particular of 5 tones and 2 semitones in the next order (not counting their cyclic permutations that produce the different diatonic modes)
1) Western Diatonic=2-2-1-2-2-2-1 (e.g. C D E F G A B /C). This scale is optimal at the next aspect: It has the maximum number of major and minor triad-chords.About playing it it see post 4.
Notice that the diatonic scale is not directly identical with its reverse order , but it is identical with one of its cyclic permutations (e.g. starting from F ), therefore it is considered inverse-symmetric
But are there more scales (not counting their cyclic permutations that would produce their different modes) made also from successive steps of one tone or one semitone? From the mathematical point of view it is easy to find them all.
We are restricting to 7-notes scales
At first we notice that as it is a 7-notes scale it cannot have more than 5 whole notes but neither less than 5 whole notes, as this wold not give in total 12 semitones with 7 addition terms.
Therefore all such scales would be permutations of the pattern 2-2-1-2-2-2-1.
In particular all of them would have 2 semitones!.Now these semitones may be separated by 2 or 3 tones as in the diatonic scale, or by one only semitone or by zero semitones. This gives two other scales.
2) Minor melodic=(1-2-1-2-2-2-2) and all cyclic permutations of it that give its modes (known also as Hindu scale see http://www.scales-chords.com/) , This scale is identical with its inverse order
and the
3) Altered natural or second minor melodic or leading whole tone or Arabian scale or Neopolitan major =(1-1-2-2-2-2-2) and all cyclic permutations of it that give its modes. Again this scale is identical with its inverse order.
I found the term altered natural in the next classification list https://psg.com/~dlamkins/lamkins-guitar/Tools/scales.html and http://www.scales-chords.com/
It seems to me that besides the harmonic minor and Romani double minor, Stephan Grappelli and Django Reinhardt were using these two scales together with 8-notes scales made only from tones and semitones (see 10 of them below) in their improvisational embellishments. Stephan Grappelli soloing is utilizing the diatonic speed , with almost no (middle harmonic speed) waving but approximation of continuous movements at diatonic speed together with occasional spike jump intervals at high harmonic speed or even higher jumps.
Nevertheless if we do not restrict to 7-notes scales then of course there are more.
For example we may also classify all 8-notes scales made only from semitones and tones:
There are at least 10 such!
1) The 8-notes scale 1-1-1-1-2-2-2-2 and non-cyclic permutations of them like
2) 2-1-2-1-2-1-2-1 (diminished scale see https://en.wikipedia.org/wiki/Octatonic_scale ) .
3) Also the 8-tones Spanish or Jewish 1-2-1-1-1-2-2-2
4) and the 8-notes Jewish (Abot) (inverse of 8-notes Spanish-Jewish)1-2-1-2-2-2-1-1
(For Spanish-Jewish music see https://www.youtube.com/watch?v=f5cdoq8on1w&list=PLFEBD04189100E6EC&index=29 )
5) and the Japanese 8-tones Ichikosucho 2-2-1-1-1-2-2-1 (it is self inverse) e.g. (C D E F G A A# B C)
6) 1st Alternative of Spanish-Jewish 8-notes 1-1-2-1-1-2-2-2 (again it is self inverse)
7) 2nd Alternative of Spanish-Jewish 8-notes 1-1-2-2-1-1-2-2 (again self inverse)
8) 3rd Alternative of Spanish-Jewish 8-notes An extrapolation of the diatonic scale 2-2-1-2-2-2-1 and of the Harmonic minor scale (2-2-1-3-1-2-1) to an 8 notes scale made by
2-2-1-2-1-1-2-1 (C D E F G G# A B C) (it is self-inverse) In this scale the chord progression of the Andaluzian Cadenza fits exactly
9) 4th Alternative of Spanish-Jewish 8-notes (1-2-1-1)-2-(2-1-2)
10) 5th Alternative of Spanish-Jewish 8-notes 1-2-2-1-1-2-1-2 (inverse of the previous)
We may compare them with the
1-3-1-1-1-1-3-1
and the 10-notes scale 1-1-1-1-1-1-2-1-2-2
All the above scales may be considered extrapolations to intervals of only 1,2 semitones, of arpeggios of 3-notes chords of the type major,minor, diminished and augmented.
The chords of the 8-notes Spanish-Jewish are the next when starting from C
| Notes of this scale: |
| C; C#/Db; D#/Eb; E; F; F#/Gb; G#/Ab; A#/Bb; C; |
| Interval structure of this scale: |
| h W h h h W W W |
| Chords that fit in this scale: |
| Normal Triads: C# C#m Caug Cdim D#m Eaug Fm F# G# G#aug A#m A#dim Other Triads: C#sus4 C#sus2 D#sus4 D#sus2 Fsus4 F#sus2 G#sus4 G#sus2 A#sus4 A#sus2 4 Notes Chords: C7b5 C7#5 C#6 C#m6 C#maj7 C#m(maj7) Cm7b5 D#m6 D#m7 D#7sus4 D#7sus2 Fm7 Fm(maj7) F7sus4 F#6 F#maj7 F#7 F#7b5 F#7sus2 G#6 G#7 G#7#5 G#7sus4 G#7sus2 A#m7 A#m7b5 A#7sus4 A#7sus2 |
Also 9- notes scales like 2-2-1-2-1-1-1-1-1 or 2-1-1-2-1-1-2-1-1 and non-cyclic permutations of them.
E.g. The 9-tones Moorish Phrygian =1-2-1-1-2-1-2-1-1
or 9-tones scales like 2-1-1-1-2-2-1-1-1 (C, D, D# ,E F, G A A# B C)
or 9-tones scales like 2-1-2-1-1-1-2-1-1 which is an extrapolation from the Harmonic double minor 2-1-3-1-1-3-1
We may compare these scales also with the Chinese 5-notes scales that have 2-tones steps , in other words interval structure
Interval fro the root : 1, 3, #4, 5, 7
Intervals in steps: 4 - 2 - 1 - 4 - 1
Formula: Quadra-step, Whole, Half, Quadra-step, Half
See e.g.
http://www.pianoscales.org/chinese.html
The chords that fit to the the melodic minor scale are the next: we take as example the D melodic minor
| Notes of this scale: |
| D; E; F; G; A; B; C#/Db; D; |
| Interval structure of this scale: |
| 2-1-2-2-2-2-1 |
| Chords that fit in this scale: |
| Normal Triads: C#aug C#dim Dm Em Faug G A Aaug Bdim Other Triads: Dsus4 Dsus2 Esus4 Gsus2 Asus4 Asus2 4 Notes Chords: C#7b5 C#7#5 C#m7b5 Dm6 Dm(maj7) Em6 Em7 E7sus4 G6 G7 G7b5 G7sus2 A7 A7#5 A7sus4 A7sus2 Bm7b5 |
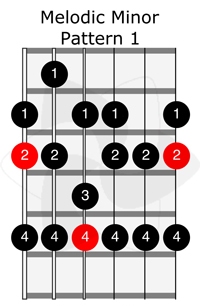
A way to play this melodic minor or Hindu scale on the 4 highest strings, with the rule of 2 notes per string is the next
The chords that fit the second melodic minor scale or also called leading whole tone scale are the next (we take the example of the C leading whole tone (or second melodic minor ) scale
| Notes of this scale: |
| C; D; E; F#/Gb; G#/Ab; A#/Bb; B; C; |
| Interval structure of this scale: |
| 2-2-2-2-2-1-1 |
| Chords that fit in this scale: |
| Normal Triads: Caug Daug E Eaug F#aug G#aug G#dim A#aug Bm Other Triads: Esus2 Bsus4 4 Notes Chords: C7b5 C7#5 D7b5 D7#5 E7 E7b5 E7#5 E7sus2 F#7b5 F#7#5 G#7b5 G#7#5 G#m7b5 A#7b5 A#7#5 Bm6 Bm(maj7) |
A way to play this previous scale sometimes cal led Arabic scale on the 4 highest strings, with the rule of 2 notes per string is the next
The next are 5 ways to play on the guitar fretboard the melodic minor scale
On the higher 4 strings of the guitar (or on a ukulele or on a 4-string Buzuki) the next is the pattern on the fretbaord of the second melodic or leading whole tones scale (although without the notes names that would not be accurate on the strings as the ukulele is tuned a bit higher than the guitar)
We may compare these scales also with the Chinese 5-notes scales that have 2-tones steps , in other words interval structure
Interval fro the root : 1, 3, #4, 5, 7
Intervals in steps: 4 - 2 - 1 - 4 - 1
Formula: Quadra-step, Whole, Half, Quadra-step, Half
See e.g.
http://www.pianoscales.org/chinese.html
For example if we take the mode of the diatonic scale starting from F
F G A B C D E F , a Chinese scale will be shaped by keeping the semitones B C,, E, F, but eliminating the notes G, D , Thus it will be
F, A, B, C, E,
All 7-notes scales made from semitones, tones and at least one 3-semitone.
Many such scales are used in the Greek folk music with Buzuki, and have their origin in ancient Greece, Byzantine empire, and Arabic music. Many of them have Arabic names although they are played on the 12-semitone Bach equal temperament scale.
For the names of some of these scales see http://www.scales-chords.com/
Therefore its is worth finding them all. We have already found all of them that they do not contain a 3-semitone (see post 51, the diatonic, the melodic minor and the second melodic minor) . So let us find all that contain at least one 3-semitone We already know so far
1) the Harmonic minor= (1-3-1)-2-(-1-2-2), and
2)the Romani (or Hungarian /Ukrainian/Flamenco) double minor (modes also of Niavent and Hijaskar) also called Byzantine or Harmonic double minor scale (and by some also called abydos Egyptin scale)=(1-3-1)-2-(-1-3-1) (notice that the inverse order of it is identical with it).
The Romanian kaval flutes with 5 holes play the 6-notes scale 2-1-3-1-1-4 E.G. A4-B4-C5-D#5-E5-F5-A5 and by adding a 6th thump hole to play the G5# it becomes a Harmonic double minor scale A4-B4-C5-D#5-E5-F5-G5#-A5 or 2-1-3-1-1-3-1 which is a mode of the E5 harmonic double minor scale.
3) A slight alternation of it is the Persian scale or todi theta scale=(1-3-1-1-2-3-1)
4) Inverse Persian scale or Purvi Theta scale (3-1-1-3-2-1-1) or Byzantine parachromatic scale
The last 3 contain two 3-semitones, but only the Harmonic double minor two tetrachords 1-3-1 ! And the other two scales of post 50 are
This scale (as the harmonic double minor or Byzantine double minor too) too is directly derivable from the pentatonic scale e.g., the Egyptian mode of it 2-3-2-3-2 gives the
2-1-1-3-1-1-3 This scale can be easily played in the Shakuhachi minor pentatonic flutes.
5) the 2nd Harmonic minor or Kurdi or Kassigar=(1-3-1)-2-(-2-1-2) (which is the inverse order of the Harmonic minor),
6) and the 3rd Harmonic minor or Shamba (which is the inverse of the Neopolitan scale below) =(1-3-1)-2-(-2-2-1)
all of them containing the oriental tetra-chord 1-3-1.
We may take the inverse order of the Shamba which is called the Neopolitan scale
7) The 4th Harmonic minor or Neapolitan scale (different from the major and the minor Neopolitan)= (1-3-1)-1-(-2-2-2)
Notice that the Neapolitan scale is made by the inverses of 2 ancient Greek tetrachords the 1-1-3 and the 1-2-2 withe and in between tone 2 (disjunction of tetrachords or divorced tetrachords) . The 1-1-3 was called in ancient Greece the tonal tetrachor of the Chromatic Generation and the 1-2-2 the syntono tetrachord of the Diatonic generation.
Now are there more? Certainly there are! Many of them are modern versions in the 12-semitones scale realizations of ancient Byzantine 7-notes scales or "sounds" (ηχοι). If there are two 3-semitones as in the Romani double minor, we may have a permutation of it , which is not a cyclic permutation (mode of the Romani double minor) which are the next
8) (3-1-3-2-1-1-1)
9) Second Harmonic or Romani double minor=(3-1-3-1-2-1-1) or gypsy hexatonic or Mela Gayakapriya, Raga Kalakanti (see post 227 )
10) Third Harmonic or Romani double minor=(3-1-3-1-1-2-1) inverse of Mela Ganamurti, Raga Ganasamavarali (see post 227)
11) (3-1-3-1-1-1-2)
12) (3-1-2-3-1-1-1)
The next scales do not sound too much as minor scales as the 3-3 , or 3-2-3 is not sad and are mainly extrapolations of the western or Chinese/Mongolian pentatonic !
13) (3-2-3-1-1-1-1) (with a very peculiar sound)
14) (3-2-1-3-1-1-1)
15) (3-3-2-1-1-1-1) (with a very peculiar sound)
16) (3-3-1-2-1-1-1)
17) (3-3-1-1-2-1-1)
18) (3-3-1-1-1-2-1)
19) (3-3-1-1-1-1-2) (this is the inverse order of scale 15)
While if it has only one 3-semitone we may take non-cyclic permutations of the 3) and 4) like the next fr which ma nor aware of names, but maybe there are in modern Arabic music (At first we make all possible combinations of different intervals around 3, and then all possible non-cyclic permutations of the rest of the intervals)
20) (1-3-2)-1-(-2-1-2)
21) (1-3-2)-1-(-1-2-2)
22) (1-3-2)-2-(-1-1-2)
23) Called Enigmatic (1-3-2)-2-(-2-1-1)
24) (1-3-2)-2-(-1-2-1) Anasazi flute scale or
| Mela Vanaspati, Raga Bhanumati |
26) (2-3-1)-1-(-2-1-2)
27) (2-3-1)-1-(-1-2-2) Inverse Anasazi flute scale or inverse
| Mela Vanaspati, Raga Bhanumati |
29) (2-3-1)-2-(-2-1-1)
30) Called Hungarian major scale (2-3-1)-2-(-1-2-1)
31) (2-3-1)-1-(-2-2-1) This scale is
refered in this video https://www.youtube.com/watch?v=mjttaiOq-8Q
as the 7-notes soul scale and is refred as the major pentatonic scale with added flat 3rd and flat 7nth!
32) (2-3-2)-1-(-2-1-1)
33) (2-3-2)-1-(-1-1-2)
34) (2-3-2)-1-(-1-2-1)
35) (2-3-2)-2-(-1-1-1)
It is clear that these scales can be ordered according to how many usual chords they define (like major, minor diminished, augmented). The more non-weird chords the higher in the list. In other words they are not all of them the same good from the point of view of harmony of the chords they define, although they may seem very similar from the melodic point of view.
There are also the 6 notes Hirajoshi scale
http://www.flutopedia.com/scale_Hirajoshi_Extended.htm
and the Miyako Bushi extended scale
There are also the 6 notes Hirajoshi scale
http://www.flutopedia.com/scale_Hirajoshi_Extended.htm
and the Miyako Bushi extended scale
It is clear that these scales can be ordered according to how many usual chords they define (like major, minor diminished, augmented). The more non-weird chords the higher in the list. In other words they are not all of them the same good from the point of view of harmony of the chords they define, although they may seem very similar from the melodic point of view.
Tetra-chords (all the next are diatonic tetra-chords)
Rast 2-2-1
Ussak 1-2-2
Kurdi 2-1-2
The next is from the second melodic minor or leading whole tone scale
Shamba 2-1-1
The next contain a 3-semitone
Niavent 2-1-3
Hijazz 1-3-1
Huzam 3-1-1
Piraeus 1-3-2
And the next are 5-notes sub-scales (penta-chords) that are essentially diatonic
Rast 2-2-1-2
Ussak 1-2-2-2
Kurdi 2-1-2-1 (this is from the melodic minor)
Minor 2-1-2-2
The next contain a 3-semitone
Shamba 2-1-1-3
Nikriz 2-1-3-1
Hijazz 1-3-1-2
Huzam 3-1-1-2
See also https://www.youtube.com/watch?v=B6xddWJFmt8
For Arabic names of many of the previous scales see
http://www.maqamworld.com/
And if we restrict to only 4-notes sub-scales (tetra-chords) , having inverse such scales not different, then we are left with a small number of 10 of such characteristic tetra-chords
They are also all such tetra-chords containing intervals of 1,2,3, and where inverses and cyclic permutations of them do not count as different . Obviously all of the above scales are compositions of two of them, with possibly an extra interval between them
Diatonic
They are also all such tetra-chords containing intervals of 1,2,3, and where inverses and cyclic permutations of them do not count as different . Obviously all of the above scales are compositions of two of them, with possibly an extra interval between them
Diatonic
2-2-1, (major, natural minor Rast, Ussak)
2-2-2, (major, augmented)
Melodic minor, double minor (Shabach)
1-2-1
Harmonic minor (Hijazz,Huzam)
1-3-1
Harmonic double minor
1-2-3,
Diminished
Diminished
3-3-3 , (diminished 7nth)
3-3-1,
Pentatonic
3-3-2,
2-2-3
2-2-3
Chromatic
1-1-1
Ir is obvious also that by extrapolating the steps 3-semitones to 2+1 we get 8-notes and 9-notes scales that are made only from steps of 1 and 2 semitones.
For a list of scales with their chords see http://www.scales-chords.com/
We may compare these scales with the 6-notes minor blue scale with interval structure
3-2-1-1-3-2 (see e.g. http://www.jazzguitar.be/minor-blues-scale.html )
or https://en.wikipedia.org/wiki/Hexatonic_scale
which is analysis of the western pentatonic below.
The 6-tone scale 1-3-3-1-3-1, the inverse which is 1-3-1-3-3-1 and the
1-3-1-3-1-3
And the 6-tone scale of the Hang instrument (raised Celtic minor )(see https://en.wikipedia.org/wiki/Hang_(instrument) )
2-1-2-2-2-3
This 6-tone Hang-scale can be derived from the dominant pentatonic
3-3-2-2-2 by splitting the 3 o 2-1, or can be derived also
from the 7-tone diatonic scale 2-1-2-2-2-1-2 by merging 1-2 to 3.
Or the 5-tone Egyptian / Mongolian mode of the western pentatonic 2-3-2-3-2
The pentatonic scale is the arpeggio of a major chord with 6th and 9th (or 2nd) which is the usual pentatonic scale
2-2-3-2-3.
Here also we may mention the blue arpeggio (arpeggio of both minor and major chord) of a chord with 6th, which is a pentatonic scale of the next structure
3-1-3-2-3
which can be considered as the harmonic minor that we subtracted the 4th and 7nth note!
The 6-tone Prometheus 2-2-2-3-1-2
The 6-tones inverse Prometheus 2-1-3-2-2-2
or the 6-tone 2-3-2-2-1-2 (raised Celtic Minor ) which is extrapolation of the 5-tonic
We may compare these scales with the Western pentatonic scale that has also two 3-semitones, that is of interval step structure 2-2-3-2-3 (also known as Egyptian/Mongolian).
Or compare them with the oriental 6-note scale 1-3-1-3-1-3
Or compare them with other 4-notes scales like 3-3-3-3
the 3-5-3-1 and 2-1-4-5 or 3-2-2-5 or 4-2-1-5, and 2-2-3-5 that extrapolations to 4-notes scales of 3-notes major or minor chords arpeggios-scales
Or the 8-notes Algerian=2-1-2-1-1-1-3-1
Or the 8-notes extrapolation of the Romani double minor
1-3-1-1-1-1-3-1
Or the Chinese 5-notes scale that have 2-tones steps , in other words interval structure
Interval fro the root : 1, 3, #4, 5, 7
Intervals in steps: 4 - 2 - 1 - 4 - 1 (the tetra-chord 1-4-1 is used instead of the oriental
1-3-1)
Formula: Quadra-step, Whole, Half, Quadra-step, Half 4 - 2 - 1 - 4 - 1
See e.g.
http://www.pianoscales.org/chinese.html
C: C, E, F#, G, B, C (we notice that it is a sub-scale of the F-major 7-notes scale)
For example if we take the mode of the diatonic scale starting from F
F G A B C D E F , a Chinese scale will be shaped by keeping the semitones B C,, E, F, but eliminating the notes G, D , Thus it will be
F, A, B, C, E, / F
Somehow all the above scales may be considered extrapolations of arpeggios of 3-notes chords of the type major,minor, diminished and augmented.
If we ask to find all scales that use steps of only 2 or 3 semitones, then they must be 5-tonic or 6-notes and the next are all the possible cases
5-tonic
3-3-2-2-2 dominant pentatonic
2-3-2-3-2 pentatonic
6-notes
2-2-2-2-2-2 (Whole tone)