As it is known the diatonic scale (major or minor mode) is made from successive steps of one tone or one semitone. In particular of 5 tones and 2 semitones in the next order (not counting their cyclic permutations that produce the different diatonic modes)
1) Western Diatonic=2-2-1-2-2-2-1 (e.g. C D E F G A B /C). This scale is optimal at the next aspect: It has the maximum number of major and minor triad-chords.About playing it it see post 4.
Notice that the diatonic scale is not directly identical with its reverse order , but it is identical with one of its cyclic permutations (e.g. starting from F ), therefore it is considered inverse-symmetric
But are there more scales (not counting their cyclic permutations that would produce their different modes) made also from successive steps of one tone or one semitone? From the mathematical point of view it is easy to find them all.
We are restricting to 7-notes scales
At first we notice that as it is a 7-notes scale it cannot have more than 5 whole notes but neither less than 5 whole notes, as this wold not give in total 12 semitones with 7 addition terms.
Therefore all such scales would be permutations of the pattern 2-2-1-2-2-2-1.
In particular all of them would have 2 semitones!.Now these semitones may be separated by 2 or 3 tones as in the diatonic scale, or by one only semitone or by zero semitones. This gives two other scales.
2) Minor melodic=(1-2-1-2-2-2-2) and all cyclic permutations of it that give its modes (known also as Hindu scale see http://www.scales-chords.com/) , This scale is identical with its inverse order
and the
3) Altered natural or second minor melodic or leading whole tone or Arabian scale or Neopolitan major =(1-1-2-2-2-2-2) and all cyclic permutations of it that give its modes. Again this scale is identical with its inverse order.
I found the term altered natural in the next classification list https://psg.com/~dlamkins/lamkins-guitar/Tools/scales.html and http://www.scales-chords.com/
It seems to me that besides the harmonic minor and Romani double minor, Stephan Grappelli and Django Reinhardt were using these two scales together with 8-notes scales made only from tones and semitones (see 10 of them below) in their improvisational embellishments. Stephan Grappelli soloing is utilizing the diatonic speed , with almost no (middle harmonic speed) waving but approximation of continuous movements at diatonic speed together with occasional spike jump intervals at high harmonic speed or even higher jumps.
Nevertheless if we do not restrict to 7-notes scales then of course there are more.
For example we may also classify all 8-notes scales made only from semitones and tones:
There are at least 10 such!
1) The 8-notes scale 1-1-1-1-2-2-2-2 and non-cyclic permutations of them like
2) 2-1-2-1-2-1-2-1 (diminished scale see https://en.wikipedia.org/wiki/Octatonic_scale ) .
3) Also the 8-tones Spanish or Jewish 1-2-1-1-1-2-2-2
4) and the 8-notes Jewish (Abot) (inverse of 8-notes Spanish-Jewish)1-2-1-2-2-2-1-1
(For Spanish-Jewish music see https://www.youtube.com/watch?v=f5cdoq8on1w&list=PLFEBD04189100E6EC&index=29 )
5) and the Japanese 8-tones Ichikosucho 2-2-1-1-1-2-2-1 (it is self inverse) e.g. (C D E F G A A# B C)
6) 1st Alternative of Spanish-Jewish 8-notes 1-1-2-1-1-2-2-2 (again it is self inverse)
7) 2nd Alternative of Spanish-Jewish 8-notes 1-1-2-2-1-1-2-2 (again self inverse)
8) 3rd Alternative of Spanish-Jewish 8-notes An extrapolation of the diatonic scale 2-2-1-2-2-2-1 and of the Harmonic minor scale (2-2-1-3-1-2-1) to an 8 notes scale made by
2-2-1-2-1-1-2-1 (C D E F G G# A B C) (it is self-inverse) In this scale the chord progression of the Andaluzian Cadenza fits exactly
9) 4th Alternative of Spanish-Jewish 8-notes (1-2-1-1)-2-(2-1-2)
10) 5th Alternative of Spanish-Jewish 8-notes 1-2-2-1-1-2-1-2 (inverse of the previous)
We may compare them with the
1-3-1-1-1-1-3-1
and the 10-notes scale 1-1-1-1-1-1-2-1-2-2
All the above scales may be considered extrapolations to intervals of only 1,2 semitones, of arpeggios of 3-notes chords of the type major,minor, diminished and augmented.
The chords of the 8-notes Spanish-Jewish are the next when starting from C
| Notes of this scale: |
| C; C#/Db; D#/Eb; E; F; F#/Gb; G#/Ab; A#/Bb; C; |
| Interval structure of this scale: |
| h W h h h W W W |
| Chords that fit in this scale: |
| Normal Triads: C# C#m Caug Cdim D#m Eaug Fm F# G# G#aug A#m A#dim Other Triads: C#sus4 C#sus2 D#sus4 D#sus2 Fsus4 F#sus2 G#sus4 G#sus2 A#sus4 A#sus2 4 Notes Chords: C7b5 C7#5 C#6 C#m6 C#maj7 C#m(maj7) Cm7b5 D#m6 D#m7 D#7sus4 D#7sus2 Fm7 Fm(maj7) F7sus4 F#6 F#maj7 F#7 F#7b5 F#7sus2 G#6 G#7 G#7#5 G#7sus4 G#7sus2 A#m7 A#m7b5 A#7sus4 A#7sus2 |
Also 9- notes scales like 2-2-1-2-1-1-1-1-1 or 2-1-1-2-1-1-2-1-1 and non-cyclic permutations of them.
E.g. The 9-tones Moorish Phrygian =1-2-1-1-2-1-2-1-1
or 9-tones scales like 2-1-1-1-2-2-1-1-1 (C, D, D# ,E F, G A A# B C)
or 9-tones scales like 2-1-2-1-1-1-2-1-1 which is an extrapolation from the Harmonic double minor 2-1-3-1-1-3-1
We may compare these scales also with the Chinese 5-notes scales that have 2-tones steps , in other words interval structure
Interval fro the root : 1, 3, #4, 5, 7
Intervals in steps: 4 - 2 - 1 - 4 - 1
Formula: Quadra-step, Whole, Half, Quadra-step, Half
See e.g.
http://www.pianoscales.org/chinese.html
The chords that fit to the the melodic minor scale are the next: we take as example the D melodic minor
| Notes of this scale: |
| D; E; F; G; A; B; C#/Db; D; |
| Interval structure of this scale: |
| 2-1-2-2-2-2-1 |
| Chords that fit in this scale: |
| Normal Triads: C#aug C#dim Dm Em Faug G A Aaug Bdim Other Triads: Dsus4 Dsus2 Esus4 Gsus2 Asus4 Asus2 4 Notes Chords: C#7b5 C#7#5 C#m7b5 Dm6 Dm(maj7) Em6 Em7 E7sus4 G6 G7 G7b5 G7sus2 A7 A7#5 A7sus4 A7sus2 Bm7b5 |
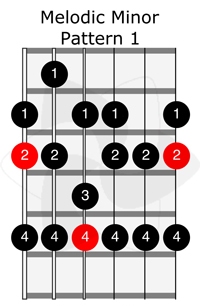
A way to play this melodic minor or Hindu scale on the 4 highest strings, with the rule of 2 notes per string is the next
The chords that fit the second melodic minor scale or also called leading whole tone scale are the next (we take the example of the C leading whole tone (or second melodic minor ) scale
| Notes of this scale: |
| C; D; E; F#/Gb; G#/Ab; A#/Bb; B; C; |
| Interval structure of this scale: |
| 2-2-2-2-2-1-1 |
| Chords that fit in this scale: |
| Normal Triads: Caug Daug E Eaug F#aug G#aug G#dim A#aug Bm Other Triads: Esus2 Bsus4 4 Notes Chords: C7b5 C7#5 D7b5 D7#5 E7 E7b5 E7#5 E7sus2 F#7b5 F#7#5 G#7b5 G#7#5 G#m7b5 A#7b5 A#7#5 Bm6 Bm(maj7) |
A way to play this previous scale sometimes cal led Arabic scale on the 4 highest strings, with the rule of 2 notes per string is the next
The next are 5 ways to play on the guitar fretboard the melodic minor scale
On the higher 4 strings of the guitar (or on a ukulele or on a 4-string Buzuki) the next is the pattern on the fretbaord of the second melodic or leading whole tones scale (although without the notes names that would not be accurate on the strings as the ukulele is tuned a bit higher than the guitar)
We may compare these scales also with the Chinese 5-notes scales that have 2-tones steps , in other words interval structure
Interval fro the root : 1, 3, #4, 5, 7
Intervals in steps: 4 - 2 - 1 - 4 - 1
Formula: Quadra-step, Whole, Half, Quadra-step, Half
See e.g.
http://www.pianoscales.org/chinese.html
For example if we take the mode of the diatonic scale starting from F
F G A B C D E F , a Chinese scale will be shaped by keeping the semitones B C,, E, F, but eliminating the notes G, D , Thus it will be
F, A, B, C, E,