This book is for learning music composition and improvisation , based on more abstract mathematics of the music, the rhythm and the musical instrument and with new musical practice. It is a new awareness and method to link mental perception-images, the creation of feelings and finger actions. The true goal of composition and improvisation is the existential process of creating and listening it. It is both individually healing and socially celebrating.
Translate
Thursday, January 21, 2016
31. The circular ring Z(12) representation of the 12-semitones chromatic or equal temperament scale as a game. Chords melodically in series
(The post has not been written yet )
30.Transitions of chords in chord progressions . The 3 basic relations of chords.
AN EXCELLENT SOFTWARE TOOL TO UNDERSTAND THE BASIC 3 CHORD REATIONS IS THE SOFTWARE NAVICHORD (FOR IOS). IT HAS A HEXAGONIC TOUCH-SCREEN KEYBORD OF THE NOTES WHERE THE CHORDS ARE TRIAGNGLES AND ARE PLAYED BY TOUCHING THE CENTER OFTHE TRIANGLE
SUCH HEXAGONIC KEYBOARDS HAVE BEEN PATENTED ALSO IN THE TERPSTRA KEYBOARD. THE 3 BASIC LOCAL RELATIONS OF THE CHORDS (NO-COMMON NOTE OR CHROMATIC RELATION, ONE COMMON NOTE OR HARMONIC RELATION AND TWO COMMON NOTES OR MELODIC RELATION) ARE IMMEDIATELY VISIBLE.
The 3 basic harmonic relations of two successive chords are described as types of chord transitions below and are based on the 3 types of intervals 1) 4th as inverted perfect 5th 2) 3rd (either major or minor) 3) 2nd (either major or minor).
AND OBVIOUSLY, SINCE THIS IS THE ORDER OF WHICH TYPE OF INTERVALS IS MORE HARMONIC (SEE POST 40 ) THE SAME APPLIES TO THE CORD RELATIONS: RESOLUTIONAL RELATION IS MORE HARMONIC COMPARED TO RELATIVES RELATION WHICH IN ITS TURN IS MORE HARMONIC COMPARED TO DIATONIC OR COMPLEMENTARY RELATION!
The most common transitions of chords in the songs are the next 3
1) HARMONIC RELATION Successive resolutional relation of chords (Wheel of 4ths)
R1(x)-->R2(y) where R2 is a perfect forth higher than R2, and x, y define the quality of the chord as major, minor, dim, 7th etc. Of course even more often x contains a qualification as 7th chord resolving to a non-7th chord R2(y). E.g. G7-->C, or A7-->Dm etc
MAIN UTILITY: The main advantage of this chord transition is that with just the two chords we practically cover all the notes (except one) of a diatonic scale, and both the chords can be major or both can minor or alternating. We cover with such chord transitions melodies that may aextend a whole octave or more. By extending the first to dominant 7th chords we get also the emotion of anxiety resolution to serenity.
MELODIC MEANING : When such a pair of chords accompanies a melody then taking the themes of this melody either the theme is inside the chords is or is a bridge theme relating the two chords. This means that either the interval of 5 (4th) or 7 semitones (5th) appears as a shift or translation of the theme (chord-theme) or exists inside the theme (bridge-theme).
EMOTIONAL TRANSITION: The emotional impact is as it is very well known the resolution from anxiety to serenity (e.g. E7->Α). The reverse order has reverse emotional impact , but here enter the ingenious tricks of harmonic resolutions inversions (see post 29)
RELEVANT MELODIC DENSITY OR SPEED: The relevant melodies are the high harmonic density or high harmonic melodic speed (see post 68 ). Usually the notes x1,x2 of the simplicial submelody (see posts 9, 72 ) that correspond to the two chords of this transition are either an interval of 4th (5 semitones) apart or 1 semitone apart.
In the symbolism of the post 23 of the chords as positioned by shape on the fretboard,
the next are in the resolutional relation relation
The (nE)X major chord (which means the chord of E shape at the nth fret, and that sounds like X) resolves to the major chord ((n)A)Y while the relative to the same corresponding relative.
The (nA)X major chord (which means the chord of A shape at the nth fret, and that sounds like X) resolves to the major chord ((n)D)Y while the relative to the same corresponding relative.
The (nD)X major chord (which means the chord of D shape at the nth fret, and that sounds like X) resolves to the major chord ((n+2)E)Y while the relative to the same corresponding relative.
Obviously the sequence of the letters in the term DAE system, is the reverse order of the successive resolutions relations (E->A->D)
R1(x)-->R2(y) where R2 is a perfect forth higher than R2, and x, y define the quality of the chord as major, minor, dim, 7th etc. Of course even more often x contains a qualification as 7th chord resolving to a non-7th chord R2(y). E.g. G7-->C, or A7-->Dm etc
MAIN UTILITY: The main advantage of this chord transition is that with just the two chords we practically cover all the notes (except one) of a diatonic scale, and both the chords can be major or both can minor or alternating. We cover with such chord transitions melodies that may aextend a whole octave or more. By extending the first to dominant 7th chords we get also the emotion of anxiety resolution to serenity.
MELODIC MEANING : When such a pair of chords accompanies a melody then taking the themes of this melody either the theme is inside the chords is or is a bridge theme relating the two chords. This means that either the interval of 5 (4th) or 7 semitones (5th) appears as a shift or translation of the theme (chord-theme) or exists inside the theme (bridge-theme).
EMOTIONAL TRANSITION: The emotional impact is as it is very well known the resolution from anxiety to serenity (e.g. E7->Α). The reverse order has reverse emotional impact , but here enter the ingenious tricks of harmonic resolutions inversions (see post 29)
RELEVANT MELODIC DENSITY OR SPEED: The relevant melodies are the high harmonic density or high harmonic melodic speed (see post 68 ). Usually the notes x1,x2 of the simplicial submelody (see posts 9, 72 ) that correspond to the two chords of this transition are either an interval of 4th (5 semitones) apart or 1 semitone apart.
In the symbolism of the post 23 of the chords as positioned by shape on the fretboard,
the next are in the resolutional relation relation
The (nE)X major chord (which means the chord of E shape at the nth fret, and that sounds like X) resolves to the major chord ((n)A)Y while the relative to the same corresponding relative.
The (nA)X major chord (which means the chord of A shape at the nth fret, and that sounds like X) resolves to the major chord ((n)D)Y while the relative to the same corresponding relative.
The (nD)X major chord (which means the chord of D shape at the nth fret, and that sounds like X) resolves to the major chord ((n+2)E)Y while the relative to the same corresponding relative.
Obviously the sequence of the letters in the term DAE system, is the reverse order of the successive resolutions relations (E->A->D)
2) MELODIC RELATION Relative chords (Wheel of 3rds)
R1(x)-->R2(y) where R2 is a minor or major one interval of 3rd lower than R1, or a major or minor 3rd higher than R1, defining thus that the two chords are relatives (normally with two common notes) . Or R1=R2 but R1(x) is major and R2(y) is minor or versa,in other words relative chords with the same root. . Most often of course normally, the first is major and the second minor and vice versa. E.g. C-->Am or
R1(x)-->R2(y) where R2 is a minor or major one interval of 3rd lower than R1, or a major or minor 3rd higher than R1, defining thus that the two chords are relatives (normally with two common notes) . Or R1=R2 but R1(x) is major and R2(y) is minor or versa,in other words relative chords with the same root. . Most often of course normally, the first is major and the second minor and vice versa. E.g. C-->Am or
C-->Em, or Em-->G.
MAIN UTILITY: The main advantage of this chord transition is that we may pass from a minor to a major or vice-versa, thus change from sadness to joy or vice-versa with slight only change of the notes of the melody and the chord!
MELODIC MEANING: When such a pair of chords accompanies a melody then taking the themes of this melody either the theme is inside the chords is or is a bridge theme relating the two chords. This means that either the interval of 3 (minor 3rd) or 4 semitones (major 3rd) appears as a shift or translation of the theme (chord-theme) or exists inside the theme (bridge-theme).
EMOTIONAL TRANSITION: The emotional impact depends to if we pass from a major to minor or from minor to major. When we pass from major to one of its three relative minors is a transition from joy to sadness and vice versa when we pass from a minor to one of its three relative majors.
RELEVANT MELODIC DENSITY OR SPEED: The relevant melodies are the middle harmonic density or middle harmonic melodic speed (see post 68 ).Usually the notes x1,x2 of the simplicial submelody (see posts 9, 72 ) that correspond to the two chords of this transition are either an interval of 3rd (3 or 4 semitones) apart, and at least one of them is a non-common note.
All the above three relations support the declaration of melodic bridge from harmonic speed to diatonic speed.Often melodic bridges from a chord to the next, may start with harmonic speed or density covering the first chord A and then decelerate to diatonic speed or density when reaching to the next chord B.
ONLY TWO RELATIONS FOR THE HAND:
From the point of view of the hand on the fret-board and not of the ear, the relations of two chords can be simplified to only 2: 1) The resolutional (Shape E -> to shape A-> to shape D etc) and 2) The shift of the chord by a tone or semitone on the fretboard. The reason is that the 3rd relation of relative chords can be derived by combining the resolutional backwards or forwards and then shifting forwards or backwards by a tone or semitone!
This gives a practical "rule of thump" way to find chords in melody, by experimenting proceeds in the resolutional wheel of 4ths together shifts back or forth by tones or semitones to chords, and making it as local as possible if the melody has also similar local (small distance) changes.
ONLY ONE RELATIONS (the resolution or wheel of 4ths) FOR THE EAR:
From the point of view of the ear recognizes harmonically the resolution relation, that is the wheel of 4ths The reason is that the 2nd relation of complememtary can be considered as x+3 in the wheel of 4ths while 3rd relation of relative chords can be considered as the x-4 and x-5 in the wheel of 4ths. Thus all the relations translate to the resolution relation.
In the symbolism of the post 23 of the chords as positioned by shape on the fretboard,
the next are in the upper and lower relatives relation :
For the relative chords of major chords the rules are :
The (nE)X chord (which means the chord of E shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n-1)Dm)Ym (e.g. F with Dm) (or ((n+4)Am)Ym) and as upper relative chord the ((n-3)Am)Zm (or ((n+4)Em)Ym)
The (nA)X chord (which means the chord of A shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n+2)Em)Ym (e.g. A with F#m) and as upper relative chord the
((n-1)ADm)Zm
The (nD)X chord (which means the chord of D shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n+2)Am)Ym (e.g. D with Bm) and as upper relative chord the ((n+2)Em)Zm
It is easy to see that the shape of lower relative minor chord of major chord, compared to the shape of the major chord is simply the cycle of letters of the DAE system (D->A->E->D), which is the reverse order of the successive irresolution relations which is E->A->D->E . That is the lower relative minor of major D shape chord is a minor A shape chord, the lower relative minor of major A shape chord is a minor E shape chord, the lower relative minor of major E shape chord is a minor D shape chord!!! Notice also that to find the lower relatives of the vertical sequence of successive resolutional chords E,A,D on the fretboard, we only need to go either 1 step lower in the fretboard (n-1) or 2 steps higher in the fretboard (n+2).
One step lower for E and 2 steps higher for A and D, while always the shape of the relative is in the reverse order of the resolutional order E->A->D->E.
While the shape of upper relative minor chord of major chord, compared to the shape of the major chord is simply the reverse order of cycle of letters of the DAE system (D->E->A->D) exactly as in the relation of successive resolutions . That is the upper relative minor of major D shape chord is a minor E shape chord, the upper relative minor of major A shape chord is a minor D shape chord, and the upper relative minor of major E shape chord is a minor A shape chord!!!
For the relative chords of minor chords:
The (nEm)Xm chord (which means the chord of E shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n-2)D)Y and as upper relative chord the ((n-2)A)Z
The (nAm)Xm chord (which means the chord of A shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n+1)E)Y and as upper relative chord the ((n-2)D)Z
The (nDm)Xm chord (which means the chord of D shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n+1)A)Y and as upper relative chord the ((n+1)E)Z
MAIN UTILITY: The main advantage of this chord transition is that we may pass from a minor to a major or vice-versa, thus change from sadness to joy or vice-versa with slight only change of the notes of the melody and the chord!
MELODIC MEANING: When such a pair of chords accompanies a melody then taking the themes of this melody either the theme is inside the chords is or is a bridge theme relating the two chords. This means that either the interval of 3 (minor 3rd) or 4 semitones (major 3rd) appears as a shift or translation of the theme (chord-theme) or exists inside the theme (bridge-theme).
EMOTIONAL TRANSITION: The emotional impact depends to if we pass from a major to minor or from minor to major. When we pass from major to one of its three relative minors is a transition from joy to sadness and vice versa when we pass from a minor to one of its three relative majors.
RELEVANT MELODIC DENSITY OR SPEED: The relevant melodies are the middle harmonic density or middle harmonic melodic speed (see post 68 ).Usually the notes x1,x2 of the simplicial submelody (see posts 9, 72 ) that correspond to the two chords of this transition are either an interval of 3rd (3 or 4 semitones) apart, and at least one of them is a non-common note.
All the above three relations support the declaration of melodic bridge from harmonic speed to diatonic speed.Often melodic bridges from a chord to the next, may start with harmonic speed or density covering the first chord A and then decelerate to diatonic speed or density when reaching to the next chord B.
ONLY TWO RELATIONS FOR THE HAND:
From the point of view of the hand on the fret-board and not of the ear, the relations of two chords can be simplified to only 2: 1) The resolutional (Shape E -> to shape A-> to shape D etc) and 2) The shift of the chord by a tone or semitone on the fretboard. The reason is that the 3rd relation of relative chords can be derived by combining the resolutional backwards or forwards and then shifting forwards or backwards by a tone or semitone!
This gives a practical "rule of thump" way to find chords in melody, by experimenting proceeds in the resolutional wheel of 4ths together shifts back or forth by tones or semitones to chords, and making it as local as possible if the melody has also similar local (small distance) changes.
ONLY ONE RELATIONS (the resolution or wheel of 4ths) FOR THE EAR:
From the point of view of the ear recognizes harmonically the resolution relation, that is the wheel of 4ths The reason is that the 2nd relation of complememtary can be considered as x+3 in the wheel of 4ths while 3rd relation of relative chords can be considered as the x-4 and x-5 in the wheel of 4ths. Thus all the relations translate to the resolution relation.
In the symbolism of the post 23 of the chords as positioned by shape on the fretboard,
the next are in the upper and lower relatives relation :
For the relative chords of major chords the rules are :
The (nE)X chord (which means the chord of E shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n-1)Dm)Ym (e.g. F with Dm) (or ((n+4)Am)Ym) and as upper relative chord the ((n-3)Am)Zm (or ((n+4)Em)Ym)
The (nA)X chord (which means the chord of A shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n+2)Em)Ym (e.g. A with F#m) and as upper relative chord the
((n-1)ADm)Zm
The (nD)X chord (which means the chord of D shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n+2)Am)Ym (e.g. D with Bm) and as upper relative chord the ((n+2)Em)Zm
It is easy to see that the shape of lower relative minor chord of major chord, compared to the shape of the major chord is simply the cycle of letters of the DAE system (D->A->E->D), which is the reverse order of the successive irresolution relations which is E->A->D->E . That is the lower relative minor of major D shape chord is a minor A shape chord, the lower relative minor of major A shape chord is a minor E shape chord, the lower relative minor of major E shape chord is a minor D shape chord!!! Notice also that to find the lower relatives of the vertical sequence of successive resolutional chords E,A,D on the fretboard, we only need to go either 1 step lower in the fretboard (n-1) or 2 steps higher in the fretboard (n+2).
One step lower for E and 2 steps higher for A and D, while always the shape of the relative is in the reverse order of the resolutional order E->A->D->E.
While the shape of upper relative minor chord of major chord, compared to the shape of the major chord is simply the reverse order of cycle of letters of the DAE system (D->E->A->D) exactly as in the relation of successive resolutions . That is the upper relative minor of major D shape chord is a minor E shape chord, the upper relative minor of major A shape chord is a minor D shape chord, and the upper relative minor of major E shape chord is a minor A shape chord!!!
For the relative chords of minor chords:
The (nEm)Xm chord (which means the chord of E shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n-2)D)Y and as upper relative chord the ((n-2)A)Z
The (nAm)Xm chord (which means the chord of A shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n+1)E)Y and as upper relative chord the ((n-2)D)Z
The (nDm)Xm chord (which means the chord of D shape at the nth fret, and that sounds like X) has as minor lower relative chord the ((n+1)A)Y and as upper relative chord the ((n+1)E)Z
Of course the in-place change of a chord from minor or major or vice-versa is also a relation of middle relative chords.
3) CHROMATIC RELATION Complementary chords or chromatic relation of chords (Wheel of 2nds)
R1(x)-->R2(y) where R1(x) and R2(y) are of the same type,in other words both major or both minor and R1, R2 are one tone apart. If R2=R1# or R2=R1b , then we classify this relation as complementary-resolutional rather than simply complementary. In other words the chord is shifted by one semitone higher or lower, and of course most often it retains its quality as major or minor (x=y). In the rare case of the Andaluzian cadenza, the R2 is one tone lower than R1. If R2 and R1 are one step difference in a diatonic scale we say also that the R1(x), R2(y) are complementary chords as all the notes of the two chords make 6 notes all the notes of the scale except one.
MAIN UTILITY: The main advantage of this chord transition is that with just the two chords we practically cover all the notes (except one) of a diatonic scale, and we may pass from a major to a minor chord or vice versa or remain to major or minor and cover with such chord transitions melodies that may extend less than whole octave .
MELODIC MEANING: When such a pair of chords accompanies a melody then taking the themes of this melody either the theme is inside the chords is or is a bridge theme relating the two chords. This means that either the interval of 1 (minor 2nd) or 2 semitones (major 2nd) appears as a shift or translation of the theme (chord-theme) or exists inside the theme (bridge-theme).
EMOTIONAL TRANSITION: The emotional impact depends to if we pass from a major to minor and if we step one tone higher or one tone lower. When we pass from major to a minor one step lower or one step higher, it is a transition from joy to sadness. When we pass from minor to a major one step higher, it is a transition from sadness to joy.
RELEVANT MELODIC DENSITY OR SPEED: The relevant melodies are the chromatic/diatonic harmonic density or chromatic/diatonic melodic speed (see post 68 ).Usually the notes x1,x2 of the simplicial submelody (see posts 9, 72 ) that correspond to the two chords of this transition are either an interval of 2nd (1 or 2 semitones) apart.
In the symbolism of the post 23 of the chords as positioned by shape on the fretboard,
the next are in the complementary by one tone relation relation :
R1(x)-->R2(y) where R1(x) and R2(y) are of the same type,in other words both major or both minor and R1, R2 are one tone apart. If R2=R1# or R2=R1b , then we classify this relation as complementary-resolutional rather than simply complementary. In other words the chord is shifted by one semitone higher or lower, and of course most often it retains its quality as major or minor (x=y). In the rare case of the Andaluzian cadenza, the R2 is one tone lower than R1. If R2 and R1 are one step difference in a diatonic scale we say also that the R1(x), R2(y) are complementary chords as all the notes of the two chords make 6 notes all the notes of the scale except one.
MAIN UTILITY: The main advantage of this chord transition is that with just the two chords we practically cover all the notes (except one) of a diatonic scale, and we may pass from a major to a minor chord or vice versa or remain to major or minor and cover with such chord transitions melodies that may extend less than whole octave .
MELODIC MEANING: When such a pair of chords accompanies a melody then taking the themes of this melody either the theme is inside the chords is or is a bridge theme relating the two chords. This means that either the interval of 1 (minor 2nd) or 2 semitones (major 2nd) appears as a shift or translation of the theme (chord-theme) or exists inside the theme (bridge-theme).
EMOTIONAL TRANSITION: The emotional impact depends to if we pass from a major to minor and if we step one tone higher or one tone lower. When we pass from major to a minor one step lower or one step higher, it is a transition from joy to sadness. When we pass from minor to a major one step higher, it is a transition from sadness to joy.
In the symbolism of the post 23 of the chords as positioned by shape on the fretboard,
the next are in the complementary by one tone relation relation :
The (nE)X chord (which means the chord of E shape at the nth fret, and that sounds like X) has as lower tone complementary chord the ((n-2)E)Y and as upper tone complementary chord the ((n+2)E)Z
The (nA)X chord (which means the chord of A shape at the nth fret, and that sounds like X) has as lower tone complementary chord the ((n-2)A)Y and as upper tone complementary chord the ((n+2)A)Z
The (nD)X chord (which means the chord of D shape at the nth fret, and that sounds like X) has as lower tone complementary chord the ((n-2)D)Y and as upper tone complementary chord the ((n+2)D)Z
MORE ONCHORD RELATIONS AND THEIR PSYCHOLOGICAL MEANING HERE
M symbolizes major chord m the minor chord and the number in between the distance of their roots in semitones
https://www.youtube.com/watch?v=YSKAt3pmYBs
HARMONIC POLES AND HARMONIC WAVING IN THE CHORD PROGRESSION AND STRUCTURE OF THEMES IN THE MELODY:
The emotional parallel of the harmony of intervals, suggests that the chord progression and harmonic structure of the themes of the melody, waves (Harmonic waves) between the emotion of stress,intervals of 1 or 2 semitones to the pole of harmonic serenity ,intervals of 5 (4th) , 7 (5th) or 12 (octave) semitones.
Conversely any sequence of chords with the above rules defines an harmonically meaningful chord pattern for a nice song or improvisation.
The order of the "average disance" of the chords in the above 3 harmonic relations are
complementary chords< Relative chords < Successive resolutional chords
This also corresponds to the 3-melodic densities or speeds of the melodies that fit to such chord transitions of chord progressions.
1) The complementary chords in a 2-chords transition corresponds to the chromatic/diatonic melodic speed or density.
2) The relative chords in a 2-chords transition corresponds to the middle harmonic melodic speed or density.
3) The successive resolutional chords in a 2-chords transition corresponds to the high harmonic melodic speed or density.
Based on the idea of the three relations of the chords, we may compose beautiful chord progressions. Two general rules are the next:

E.g. B7->Em->Am->D7->G->Bm-> etc
E.g. The well known song of Frank Sinatra "Fly me to the moon" is using this technique in its sequence of chords
Another example is the song of Nat King Cole L.O.V.E.
(main arc is the (Em or E7)->A7->D7->G(or Bm or Gm7) ->E7 etc with backwards retraces by one chord)
E.g. D7->G ,(1 semitone apart) Db7->Fm
or D7->G, (2 semitones apart) E7->Am
or Am->D7->G, (1 semitone apart) F#7->B7->Em
1) When playing the melodies on the fretboard in the guitar, the chromatic/diatonic speed is played mainly along the length of a string, so it is the zero angle.
2) When playing the melodies on the fretboard in the guitar, the middle harmonic speed is played mainly at an angle which relative to the horizontal is about 45 degrees and moves from the keys of the guitar to the sounding body as the melody descends in pitches! This is is because it consists of intervals of 3 or 4 semitones that in two successive strings is such an angle.
3) When playing the melodies on the fretboard in the guitar, the high harmonic speed is played mainly at an vertical angle relative to the horizontal because the strings are tuned at intervals of 5 semitones (and one string in 4 semitones). Also the interval of 7 semitones (5th) when played in descending the pitches makes an angle larger than vertical or 90 degrees (e.g. 135 degrees) and moves from the the sounding body of the guitar to the keys of the guitar as the melody descends in pitches!
Nevertheless from the point of view of common notes, the relative chords have 2 common notes, then the successive resolution chords have one common note and the complementary chords none common note.
The 3 harmonic relations of chords, with of course the chord-shapes is also a method of walking inside the fretboard.
The order of the "average disance" of the chords in the above 3 harmonic relations are
complementary chords< Relative chords < Successive resolutional chords
This also corresponds to the 3-melodic densities or speeds of the melodies that fit to such chord transitions of chord progressions.
1) The complementary chords in a 2-chords transition corresponds to the chromatic/diatonic melodic speed or density.
2) The relative chords in a 2-chords transition corresponds to the middle harmonic melodic speed or density.
3) The successive resolutional chords in a 2-chords transition corresponds to the high harmonic melodic speed or density.
Based on the idea of the three relations of the chords, we may compose beautiful chord progressions. Two general rules are the next:

A11 . 1st general rule for harmonic chord progressions: Progressions by arcs in the 12-chord cycle by intervals of 4th
This cycle defines by every connected arc of it a chord progression , where a chord may be substituted with its same root relative major or minor chord , or its lower or upper minor relative chord. Of course as they are an arc of the above 12-cycle they are successive chords or in the harmonic relation of resolution.
E.g. B7->Em->Am->D7->G->Bm-> etc
Or B7->Em->Am->D7->G->C->(Am orA7)->D7 etc
E.g. The well known song of Frank Sinatra "Fly me to the moon" is using this technique in its sequence of chords
Another example is the song of Nat King Cole L.O.V.E.
(main arc is the (Em or E7)->A7->D7->G(or Bm or Gm7) ->E7 etc with backwards retraces by one chord)
A12 . 2nd general rule for harmonic chord progressions: Two arcs in the 12-chord cycle by intervals of 4th (substituting any of the chords with its minor if it is major or vice versa) that have distance at the closest ends either 1 , or 2 or 3 or 4 semitones!
E.g. D7->G ,(1 semitone apart) Db7->Fm
or D7->G, (2 semitones apart) E7->Am
or D7->G , (3 semitones apart) B7-> Em
or Am->D7->G, (1 semitone apart) F#7->B7->Em
ANGLES IN FRETBOARD AND MELODIC SPEEDS
2) When playing the melodies on the fretboard in the guitar, the middle harmonic speed is played mainly at an angle which relative to the horizontal is about 45 degrees and moves from the keys of the guitar to the sounding body as the melody descends in pitches! This is is because it consists of intervals of 3 or 4 semitones that in two successive strings is such an angle.
3) When playing the melodies on the fretboard in the guitar, the high harmonic speed is played mainly at an vertical angle relative to the horizontal because the strings are tuned at intervals of 5 semitones (and one string in 4 semitones). Also the interval of 7 semitones (5th) when played in descending the pitches makes an angle larger than vertical or 90 degrees (e.g. 135 degrees) and moves from the the sounding body of the guitar to the keys of the guitar as the melody descends in pitches!
Nevertheless from the point of view of common notes, the relative chords have 2 common notes, then the successive resolution chords have one common note and the complementary chords none common note.
The 3 harmonic relations of chords, with of course the chord-shapes is also a method of walking inside the fretboard.
THE USUAL 4 WAYS TO WALK INSIDE THE FRETBOARD ARE
1) By knowing patterns of scales
2) By known the shapes of chords, and then walk around the chord shapes
3) By knowing all the names of the notes of all the frets of the fretboard, and utilizing the 3 fretboard-neighborhoods.
4) Without any mental image, but simply by the feeling of the desired note, and the feeling-familiarization of the fretboard. At this it must be made the use of the belief that one "knows" simply by the feeling which fret sounds which note !
E.g. see https://www.youtube.com/watch?v=d7-ZnzAqt0A
The meaning of course of these 3 types of transitions is that when listening to the harmony and melody of the song, the melodically connecting element when the chord changes is 1) either a resolution in the cycle of 4ths, or 2) a relation of relatives of the chords (common notes of the chords), or 3) a small move of the root of the chord, complementary chords. Or in other words that the parallel melody during the transition of the chord most often is also doing one of the next correspondingly to the above 3 transition types 1) Moves by one semitone (resolution in the cycle of 4ths) 2) Remains the same note or moves by a 3rd (transition to a relative chord) 3) Moves by 1 semitone or by 1 tone (shift of the root of the chord by 1 semitone or 1 tone).
For the correlation of melodies with chords that fit to them, or conversely , melodies that can be improvised over a chord progression the next local concept is very significant: The melodic closure of a chord: This is defined as the closed interval of notes from all the 12-tone (chromatic) scale) with lower end the lowest note of the chord, and highest end the highest note of the chord. The chord is assumed within an octave, and normal positions, 1st inversion, and 2nd inversion have different closures. The melodic closure is also conceivable as transportable in all octaves, and not only where the chord is It holds the next interesting theorem. If we define randomly a melody within a the closure of a chord in normal position and no other note outside it, with uniform probability of occurrence of any of the notes of the closure, then according to the local condition of fit of a piece of melody with a chord the only chord in normal position that would fit this melody is the one with this as its closure!. Or more generally of we define as probabilities of sounding a note on all the octave an equal value for all notes except at the notes of the chord X where we have as probability the double this value (e.g. sound each note of the octave once but the notes of the chord twice) then any such random melody with this probability structure will have as its fitting underlying chord the chord X.
For the correlation of melodies with chords that fit to them, or conversely , melodies that can be improvised over a chord progression the next local concept is very significant: The melodic closure of a chord: This is defined as the closed interval of notes from all the 12-tone (chromatic) scale) with lower end the lowest note of the chord, and highest end the highest note of the chord. The chord is assumed within an octave, and normal positions, 1st inversion, and 2nd inversion have different closures. The melodic closure is also conceivable as transportable in all octaves, and not only where the chord is It holds the next interesting theorem. If we define randomly a melody within a the closure of a chord in normal position and no other note outside it, with uniform probability of occurrence of any of the notes of the closure, then according to the local condition of fit of a piece of melody with a chord the only chord in normal position that would fit this melody is the one with this as its closure!. Or more generally of we define as probabilities of sounding a note on all the octave an equal value for all notes except at the notes of the chord X where we have as probability the double this value (e.g. sound each note of the octave once but the notes of the chord twice) then any such random melody with this probability structure will have as its fitting underlying chord the chord X.
29. Other types of anxiety-serenity resolutions not based on diminished (and 7ths) or augmented chords, parallel resolutions and inversions of resolutions.
We had Summarized in a simplistic way the correspondence of melodic pitch dynamics and the 4-basic emotions in music (joy, sadness, anxiety, serenity) we have
1) Up pitch moves correspond to joy
2) Down pitch moves to sadness
3) Small pitch intervals of 1 or 2 semitones (chromatic or interval of 2nd) correspond to anxiety
4) Large pitch intervals (e.g. 4th, 5th octave etc) correspond to harmony and serenity.
Some instructive remarks in the composition of the melody based on the chord progression
1) In the part of the chord progression with minor chords, utilize descending melodic moves so that sadness from melody and sadness from harmony fit
2) In the sad melody parts of the melody (and minor chords) utilize rhythmic patterns that start with faster notes and end with slower notes, and the reverse for the happy part (and major chords).
3) In a triad or 7 nth 4-notes chord the most characteristic notes are the middle 2nd note (in 1-3-5 interval notation is the 3) and the 7 nth (if it exists). So for the anxiety part of the melodic moves we may utilize 1-semitone trills around these two notes, or waving with 1 or 2 semitones steps and notes outside the chord in the interval of minor 3rd (3 semitones) of the chord. Alternatively instead of trill or small amplitude waves we may utilize chromatic monotone scaling by steps of 1 semitone , or scaling with steps by intervals of 2nd of the scale, that go from these previous notes of the chord to the same such notes in the next octave. But always make sure that the notes of the chord sound in the average longer, than the notes of these anxiety transition moves with notes outside the chord.
4) Alternate up (happy) and down (sad) pitch moves , or chromatic moves (anxiety), with harmonic (on chord notes) moves (serenity-harmony).
5) Utilize at least 2 octaves, or even 3 for the melodic moves repeating the notes of the underlying chord on the next octaves , so there is sufficient space for melodic moves, to express with sufficiency the emotions.
6) For the duality of emotions anxiety-serenity, it may be utilized also harmonic waves or monotone scaling over 2 octaves at least, on the notes of the chord, but also chromatic trill wave over the notes of this wave or scaling (modulated wave on wave or move) and then return to the pure harmonic wave or scaling on the notes of the chord.
7) A chromatic wave by 1-semitones steps or all notes of the scale (steps by intervals of 2nd) that goes up and down at least 2 octaves, corresponds to a chord sub-progression of the song , of our choice that utilizes almost all the chords of the scale!
But in this post we shall talk about correlations of these emotions with the harmony not the melody of chord transitions!
Parallel or alternative resolutions: For example if G->G7 resolves to --> C, then a parallel resolution is a sequence of chords R1,R2,...Rn, with the same feeling of resolution and R1=G7, Rn=C.
The I-V-IV-V-I triple majors paralel resolution
(1M->4M->5M->1M)
e.g. D->A->G->A->D
this progression is also created when we descend or ascend by 2nds a melody (waving or not) with 2nd voice which can be extended with 3-notes or a major chord instead of 2 voices, in a diatonic scale.
Such sequences come initially from the natural progression by 2nds of the chords
e.g. I-ii-iii-IV-V-I , that by substituting minors with their relative majors becomes
I-IV-V-IV-V-I
or I-ii-iii-IV-V-vi-vii-I
I-IV-V-IV-V-IV-V-I
The I-V-IV-V-I triple majors paralel resolution
(1M->4M->5M->1M)
e.g. D->A->G->A->D
this progression is also created when we descend or ascend by 2nds a melody (waving or not) with 2nd voice which can be extended with 3-notes or a major chord instead of 2 voices, in a diatonic scale.
Such sequences come initially from the natural progression by 2nds of the chords
e.g. I-ii-iii-IV-V-I , that by substituting minors with their relative majors becomes
I-IV-V-IV-V-I
or I-ii-iii-IV-V-vi-vii-I
I-IV-V-IV-V-IV-V-I
E.g.The aug parallel resolution R1=G R2=Gaug R3=C.
Or R1=Bb, Rn=A in the Andaluzian Cadenza Dm, C, Bb A.
or 1M7->1M then 5M->5aug->1M
or 1M7->1M then 5M->5aug->1M
There are plenty many chord progressions that are parallel resolutions.
E.g. The parallel to major-major resolution the relative minor-chromatic a parallel to the G7->C is the G7->Em->B7->C or if it is the A7->D, then A7->F#m->C#7 ->D
Similarly, the parallel to a minor-minor resolution is the relative major-major resolution
E.g. parallel to the Am->Dm is the major-major resolution C->F, so in total
Am->F->C->Dm notice that we set the inverse of the relative resolution.
or if it is the major-major G->C, the relative resolution is the Am->Dm or Bm->Em, so the total will be G->Dm->Am->C or G->Em->Bm->C.
Similarly, the parallel to a minor-minor resolution is the relative major-major resolution
E.g. parallel to the Am->Dm is the major-major resolution C->F, so in total
Am->F->C->Dm notice that we set the inverse of the relative resolution.
or if it is the major-major G->C, the relative resolution is the Am->Dm or Bm->Em, so the total will be G->Dm->Am->C or G->Em->Bm->C.
The parallel to major-minor resolution chromatic- chromatic, a parallel e.g. to the resolution A7->Dm is the sequence A7->D#7->A#->Dm or A7->A#->D#7->Dm
The 1st dim7 simple chromatic parallel resolution e.g.
Instead of A7->Dm, the Edim7->Dm. Or e.g. instead of
E7->Am the Bdim7->Am.
The 2nd dim7 simple chromatic parallel resolution e.g.
Instead of A7->Dm , the Ddim7->Dm. Or e.g. instead of
E7->Am the Adim7->Am.
The 3rd dim7 simple chromatic parallel resolution
Instead of E7->A the Edim7->A (that is also why some times D#7 is considered to resolve to A, and D#7 is almost identical with the Edim7) or instead of A7->Dm the Adim7->Dm.
The 3 dim7 simple chromatic parallel resolution are not of equal intensity. Their intensity of resolutions is the order with which are presented.
The 3rd dim7 simple chromatic parallel resolution
Instead of E7->A the Edim7->A (that is also why some times D#7 is considered to resolve to A, and D#7 is almost identical with the Edim7) or instead of A7->Dm the Adim7->Dm.
The 3 dim7 simple chromatic parallel resolution are not of equal intensity. Their intensity of resolutions is the order with which are presented.
The dim7 enhanced chromatic parallel resolution e.g. Ddim7->A7->Dm
The Xm6 . minor 6th resolution:
This is a resolution with chord transition in the relation of complementary chords. In other words, the first chord is a minor and resolves to a major one tone lower, if the minor is a minor 6th: E.g. Am6->G, or Em6->D, or Dm6->C , or Gm6->F etc. This is so because the minor 6th contains already part of the 7nth of the previous chord in the wheel by 4ths e.g. D7->G, becomes Am6->G etc.
This resolutions can resolve to the relative so instead Am6->G the Am6->Em, thus it is an inversion of the Em->Am, that is mentioned below:
The extended Xm6 minor 6th resolution
This is the same as the previous but , we interpolate one more major chord at first with root one tome higher than the minor 6th and then end with the major with root one tome lower than the minor 6th e.g. Am6->B7->G, or Em6->F7->D, or Dm6->E7-C , or Gm6->A7->F , Fm6->G->Db etc.
Since the Xm6 chord is identical with the Ym7b5 chord (half diminished 7th chord) where Y is one minor 3rd lower than X, (e.g Fm6=Dm7b5) there is a natural resolution of Ym7b5 one 4th higher e.g. Dm7b5-> G, which is the interpolated chord in the extended Fm6 resolution Dm7b5=Fm6->G->Db.
The minor 6th parallel resolution with the common relative minor at 6th.
This is a resolution with chord transition in the relation one 4th back to the wheel of 4ths, thus inversion of standard resolution to minor. chords. E.g. Am6->Em, or Em6->Bm, or Dm6->Am , or Gm6->Dm etc.
The common minor as 6th parallel resolution. This is the standard resolution in the wheel by 4ths, e.g. C->F where we interpolate rge common minor relative chord when we do not want to use the first chord with 7nth, so it becomes e.g. C->Am->F or C6->F.
The Xm6 . minor 6th resolution:
This is a resolution with chord transition in the relation of complementary chords. In other words, the first chord is a minor and resolves to a major one tone lower, if the minor is a minor 6th: E.g. Am6->G, or Em6->D, or Dm6->C , or Gm6->F etc. This is so because the minor 6th contains already part of the 7nth of the previous chord in the wheel by 4ths e.g. D7->G, becomes Am6->G etc.
This resolutions can resolve to the relative so instead Am6->G the Am6->Em, thus it is an inversion of the Em->Am, that is mentioned below:
The extended Xm6 minor 6th resolution
This is the same as the previous but , we interpolate one more major chord at first with root one tome higher than the minor 6th and then end with the major with root one tome lower than the minor 6th e.g. Am6->B7->G, or Em6->F7->D, or Dm6->E7-C , or Gm6->A7->F , Fm6->G->Db etc.
Since the Xm6 chord is identical with the Ym7b5 chord (half diminished 7th chord) where Y is one minor 3rd lower than X, (e.g Fm6=Dm7b5) there is a natural resolution of Ym7b5 one 4th higher e.g. Dm7b5-> G, which is the interpolated chord in the extended Fm6 resolution Dm7b5=Fm6->G->Db.
The minor 6th parallel resolution with the common relative minor at 6th.
This is a resolution with chord transition in the relation one 4th back to the wheel of 4ths, thus inversion of standard resolution to minor. chords. E.g. Am6->Em, or Em6->Bm, or Dm6->Am , or Gm6->Dm etc.
The common minor as 6th parallel resolution. This is the standard resolution in the wheel by 4ths, e.g. C->F where we interpolate rge common minor relative chord when we do not want to use the first chord with 7nth, so it becomes e.g. C->Am->F or C6->F.
The #7 enhanced chromatic parallel resolution e.g.
A#7->A7->Dm. (4M7->3M7->6m)
The #7 simple chromatic parallel resolution e.g.
Instead of A7->Dm the D#7->Dm, Or instead of E7->Am, the A#7->Am
or instead of 3M7->6m the 7b7->6m
or instead of 3M7->6m the 7b7->6m
The relatives-sharp/flat parallel resolutions.
1) The logic of this resolution is the following: Since the major relative chord of say a minor chord has two notes in common with the minor chord, then the dominant seventh of this major relative one semitone higher or lower will have two notes, one semitone apart creating the effect of resolution.
E.g. F is relative to Dm, thus F#7->Dm and E7->Dm (4#7->2m) )will be parallel resolutions. Similarly the Bb is relative major of Dm, thus B7->Dm are a parallel resolutions. Thus we notice that not only with one step back in the cycle of 4th we have a resolution (that is A7->Dm) but also with two or three steps back we have resolutions (that is E7->Dm, B7->Dm)! And again as D is relative to Dm, then also Db7=C#7->Dm and D#7=Eb7->Dm are resolutions. Similar observations can be made with the minor relatives of major chord.
Again we may have parallel resolutions of two major chords of shift their relative minor chord by one semitone up or down. E.g. F7->D#m, F7->Dbm , Bb7->D#m, Bb7->Dbm.
As another example from the major relatives C and G of Em, we may derive the parallel resolutions C7->Fm, G7->Fm,
C7->Ebm, G7->Ebm.
2) 2nd times relatives parallel resolution: Similar to this parallel resolution is the next case . Instead of
E7->Am the E7->G->Gmaj7->G7->C->Am Or also E7->G->Gmaj7->Dm7->C->Am
Or E7->G->Gmaj7->F->C->Am. Notice that here we shift to the 2nd times relative (E7->Em->G) and we also go one step ahead in the wheel of 4ths that is to Dm7 before we return to Am. In soloing on it from the g#4 during E7 we move chromatically g#4->g4->f#4->f4->a3.
Similarly instead of D7->Gm the D7->F->Fmaj7->F7->Bb->Gm (D7->F->Fmaj7->Cm7->Gm)
Or instead of A7->Dm the A7->C->Cmaj7->C7->F->Dm (A7->C->Cmaj7->Gm7->Dm)
The two steps forward in the wheel of 4th parallel resolution
Another way to grasp the previous parallel resolution chromatic soloing g#4->g4->f#4->f4->a3. from E7 to Am , and also modify it is , to perceive it as moving two steps forward in the wheel of 4ths and move back to the resolving chord.
Thus to move from E7 to Am, we go two steps foprward in the wheel of 4ths that is (here we prefer minor) Dm, Gm , and trace it backwards Thus instead of E7->Am the E7-> Gm->Dm7->Am . Or instead of A7->Dm the A7->Cm->Gm->Dm. Instead of B7->Em the B7->Dm->Am->Em etc
2) 2nd times relatives parallel resolution: Similar to this parallel resolution is the next case . Instead of
E7->Am the E7->G->Gmaj7->G7->C->Am Or also E7->G->Gmaj7->Dm7->C->Am
Or E7->G->Gmaj7->F->C->Am. Notice that here we shift to the 2nd times relative (E7->Em->G) and we also go one step ahead in the wheel of 4ths that is to Dm7 before we return to Am. In soloing on it from the g#4 during E7 we move chromatically g#4->g4->f#4->f4->a3.
Similarly instead of D7->Gm the D7->F->Fmaj7->F7->Bb->Gm (D7->F->Fmaj7->Cm7->Gm)
Or instead of A7->Dm the A7->C->Cmaj7->C7->F->Dm (A7->C->Cmaj7->Gm7->Dm)
The two steps forward in the wheel of 4th parallel resolution
Another way to grasp the previous parallel resolution chromatic soloing g#4->g4->f#4->f4->a3. from E7 to Am , and also modify it is , to perceive it as moving two steps forward in the wheel of 4ths and move back to the resolving chord.
Thus to move from E7 to Am, we go two steps foprward in the wheel of 4ths that is (here we prefer minor) Dm, Gm , and trace it backwards Thus instead of E7->Am the E7-> Gm->Dm7->Am . Or instead of A7->Dm the A7->Cm->Gm->Dm. Instead of B7->Em the B7->Dm->Am->Em etc
The sharp/flat parallel resolution.
This is a simple logic: Instead of resolving e.g. G7->C we shift by semitone up or down the first or second chord. Thus
G#7->G7 or F#7->G7 or C#->C or B->C etc.
This can apply to 3-chord double resolutions E.g. from the standard resolution B7->E7->Am, we may derive the parallel resolution B7->F7->Am, where the last two chords happen to be relative chords too in the case of this example. Or the parallel resolution C->E7->Am, where the first and last chords in this example are relative chords.
The complementary chord parallel resolution
In this case instead e.g. resolving D7->G we utilize the upper minor complementary chord of G, here the Am instead of the D7, so the parallel resolutions is Am->G ! Notice that the Am is relative to the D7 as it has two common notes the c and a, although it is not relative to the D chord. Alternatively we may pass from the minor Am two steps back in the wheel of 4ths in other words to B7 and then to G so in total Am->B7->G.
The double major-minor enhanced resolution
e.g. instead of B7-Em, the F#7->B7-Em,or instead of
A7->Dm, the E7->A7->Dm (It is interesting to compare this also with the retraced double resolution below in other words the Gm7->A7->Dm)
The chromatic-chromatic ancenza parallel resolution. This instead of simple resolving e.g. G to C (G7->C) it starts and ends the same but as chromatic ascenza (=increasing pitch) as follows G(7)->G#(7)->B(7)->C Or instead of only D7->G, the progression D7->D#7->F#->G. This of course is the same as when we inverse he resolution So instead of G->D7, we enhance to G->F#->D#->D7.
The chromatic-diatonic ancenza parallel resolution. This instead of simple resolving e.g. G to C (G7->C) it starts and ends the same but as chromatic-diatononic ascenza (=increasing pitch AND accelerating intervals) as follows
G->G#->A#->C . Or instead of only D7->G, the progression D->D#->F->G.
Interval explanation by notes in one semitone distance
This is called the standard Dominant resolution e.g. G7->C , D7->G, C7->F etc The key to explain of this anxiety-serenity resolutions is that the dominant 7th chord e.g. G7 is the superposition of the Gmajor+Bdiminished, and the diminished chord is by itself a bit sad with anxiety, which is correlated with the Cmajor chord which has serenity because it contains at least one notes of one semitone distance of notes of the C major. These are the notes B, with one semitone distance from the C of Cmajor. The same is the explanation why the Cdim7 below resolves to G, because it has the notes D# and F# with one semitone distance from the notes D, G of Gmajor. Sometimes even Cm will be considered resolving to G, because of the D# note at one semitne distance from the D note of G, and the major chord sounds with more serenity than the minor chord!
And the same is the explanation why in the Andalusian Cadenza Dm, C, Bb A. , the Bb resolves to A, because it has 3 notes one semitone distance apart from corresponding notes of A.
Similarly as the E7 resolves to A so the Em7b5 resolves to A too because it has the 3 notes D, F , G# one semitone apart from the C#, E , A of A chord. And similarly the Edim7 resolves to A as it has the notes D, F one semitone apart from the C#, E of A
For the same reason if D7 resolves to G, then also Daug resolves to G because Daug has the notes F#, C# at one semitone distance from the notes G, D of G major chord and Daug sounds in anxiety.
Retraced double resolution. Such a phenomenon of 1-semitone apart notes we have also, if a simple resolution e.g. like A7-->Dm is enhanced to the Gm7-->A7-->Dm, or in the symbolism of the 24-cycles of chords (see post 34) in general the resolution
X7-->(x+1), is enhanced to the (x+2)7-->X7-->(x+1).
The reasons is that the (x+2)7 and X7 are complementary chords and have at least 3 notes 1-semitone apart. E.g. the Gm7, and A7 have the 3 notes (f, a#, d) of Gm 1-semitone apart of the notes (e, a, c#) of A7.
Double resolution to a minor. This is 2 major chords resolving to a minor, and the first major chord is dominant 7nth resolving to the second major chord which is also dominant seventh which in its turn resolves to the 3rd minor chord the 1st 2nd 3rd have in sequence a distance of pure forth E.g. F#7-->B7-->Em, or B7-->E7-->Am , or E7-->A7-->Dm etc
1st type of two relative resolutions
This is the case of two relative chords one minor one major, and then resolutions ending on them E.g. Em is relative to G, and we get the 1st relative resolutions B7->Em and then D7->G. For reasons of balance instead of 3 major and one minor chord we may use 2 major and 2 minor chords , thus
B7->Em, Dm7->G
2nd type of two relative resolutions
This is the case again of two relative chords one minor one major, and then resolutions on them but the first is from the first and the second resolution ends to the seconf chord E.g. Em is relative to G, and we get the 2nd relative resolutions D7->G and then Em->A. For reasons of balance instead of 3 major and one minor chord we may use 2 major and 2 minor chords, thus Dm7->G and then Em(7)->A(7)
Chromatic double minor or major resolution
This is like e.g. the B7-->E7-->A but the intermediate E7 is substituted with the chromatic in between
Bb7, so in total it is B7->Bb7->A7 and similarly for minors
instead of Bm7-->Em7-->Am , the Bm7->Bbm7->Am7
Or e.g. instead of Em7-->Am7-->Dm7, the
Em7-->D#m7-->Dm7 etc
The chord progression can be reversed too!
Resolution cycle.
This is repeated cycle of chords that at each step or piecewise at arcs it is a resolution!
E.g. G->G7->Gaug->C(1st resolution)->Cdim7->G(2nd resolution and back to the same chord)
Here a geometric representation would lead to a paradox like in a well known optical illusion as below (but here it is an emotional illusion of resolutions)
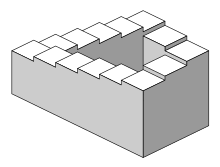
Inverse resolution= It is a sequence R1,R2,...Rn with the same feeling of resolution (from anxiety to serenity) and R1=C, Rn=G.
For example
The minor relative inversion : To inverse e.g. G-->C here are two ways
R1=C R2=Cm R3=G, or
C->Cm->C#maj7->G
or 5M7->1M inverts by 1M->1m->5M
or 5M7->1M inverts by 1M->1m->5M
or 1M->4M->4m->1M or
2m->5M inverts by 5M->5m->6M->2m
or
C-->Gm-->G7
This minor inversion of a resolution introduces the minors of the triad of major 1M, 4M, 5M
(introduces the 1m,4m,5m) which is very important in the chromatic tonality and in particular the
full chromatic tonality. The introduction of the corresponding major chords of the 3 minor chords 3m,6m,2m (to 3M,6M,2M) is done mainly by the harmonic minor and double harmonic minor instead of the natural minor in the diatonicc scale.
THUS THIS MINOR RELATIVE INVESION IS A BASIC WAY
IN CROMATIC TONALITY TO CHANGE THE 1M, 4M, 5M O MINOR CHORSD
1m-4m-5m.
The semitone-chromatic-shift major-major inversion: E.g. to invert the G7->C, we
play , C->B7->G, to invert D7->G we play G-> F#7->D. It can be written in two ways in chromatic tonality, either as 1M->7M7->5M, or as 4M->3M7->1M .
The dim7 inversion of major-major e.g. R1=C R2=Cdim7 R3=G. Or
The aug inversion of major-major e.g. R1=C, R2= Gaug R3=G
The maj7 inversion of major-minor e.g. to inverse the A7->Dm , here is a way
Dm->A#maj7->A7 (6M7->2m inverted by 2m->4maj7->3M7)
The dim7 inversion of major-minor e.g. Dm->A#dim7->A7 (6m->4dim7->3M7)
The aug inversion of major-minor e.g. Dm->Aaug->A7
The minor 6th resolution inversion as alternative resolution
This is a resolution with chord transition in the relation one 4th back to the wheel of 4ths, thus inversion of standard resolution to minor. chords. E.g. Am6->Em, or Em6->Bm, or Dm6->Am , or Gm6->Dm etc.
The minor 6th resolution inversion as alternative resolution
This is a resolution with chord transition in the relation one 4th back to the wheel of 4ths, thus inversion of standard resolution to minor. chords. E.g. Am6->Em, or Em6->Bm, or Dm6->Am , or Gm6->Dm etc.
The common minor relative chord ,inversion e.g. C->Em->G.
The relative-complementary chord inverse resolution
In this, we want e.g. to pass to inverse G7->C, so we pass to the lower relative minor of C that is to Am, then two steps back in the wheel of 4ths that is to B7 and then to G. In total
C->Am->B7->G. Or C->Am->D7->G
The relative-complementary chord inverse resolution
In this, we want e.g. to pass to inverse G7->C, so we pass to the lower relative minor of C that is to Am, then two steps back in the wheel of 4ths that is to B7 and then to G. In total
C->Am->B7->G. Or C->Am->D7->G
The 1st inverse resolution of minor-minor To inverse e.g. the minors Am->Dm here is a way Dm->Bb->E7->Am (the Dm and Bb are relative chords).
The 2nd (semitone shift) inverse resolution of minor-minor
Let us say that we want to invert the Am->Dm. We start with Dm and then we pass to the major relative F, then one semitone lower E7 and resolve to Am. In total
Dm->F->E7-Am. Other example: Gm->Bb->A7->Dm
The inverse resolution of major-minor. To inverse e.g. the E7->Am here is a way
The 2nd (semitone shift) inverse resolution of minor-minor
Let us say that we want to invert the Am->Dm. We start with Dm and then we pass to the major relative F, then one semitone lower E7 and resolve to Am. In total
Dm->F->E7-Am. Other example: Gm->Bb->A7->Dm
The inverse resolution of major-minor. To inverse e.g. the E7->Am here is a way
Am->C->B7->E7 or e.g. to inverse the A7->Dm , the Dm->F->E7->A7
The dim7 inverse resolution of major-minor e.g. to inverse the E7->Am the sequence is Am->C->Adim7->E7
or the short relative-chromatic inversion of major-minor e.g. to inverse the E7->Am,
the sequence Am-> F7->E7 (where the Am is relative to the F7, which is chromatic by a semitone to the E7) or to inverse the A7->Dm , the sequence Dm->A#->A7
The long relative-chromatic inversion of major-minor. E.g. to inverse the A7->Dm, the sequence Dm->A#->E7->A7. Or to inverse the E7->Am the sequence Am->F->B7->E7
The relative and double resolution inversion of a classical major-major resolution. To inverse e.g., the G7->C here is a way
C->A7->D7->G (Here the A7 is relative of Am which is a relative of C!)
Or C->Am7->D7->G7 or C->Am->Dm->G7
E.g, if it is to inverse E7->A, we go as follows from A we go to its relative F#m then resolve to Bm and then rrsolve to E7. So in total A->F#m->Bm->E7
or The bridge inversion of major-major C7->F-Dm7->G7 (here the C7 resolves to F which is relative to Dm7, which is relative to D7 which resolves to G7)
The short bridge inversion e.g. C7->F->G7
The long bridge inversion e.g. C->Gm->F->Dm7-G7
or C-->Cm-->F-->Dm7-->G7
And to inverse e.g. the E7-->Am , the Andalusian cadenza may be used with R1=Am, R2=G, R3=F, R4=E7.
The Bulerias inversion
E.g. to invert B7->Em
Em->Em7->A->A7->D->D7->G->G7->C->C7->B->B7
The minor-minor 7-chords Gypsy inversion
To invert the Bm->Em as follows:
Em->A7->D->G->C#7->F#7->Bm
E.g. in D major: 3m->6m is inverted by 6m->5M7->1M->4M->7M7th->3M7->6m
which is essentiall completingthe 7-chords cycle of the chords ofthe diatoninc scale.
or to invert Em->Am as follows
Am->D7->G->C->F#7->B7->Em
or to invert Am-> as follows
Dm->G7->C->F->B7->E7->Am
or
Dm->G7->C->F->Bb->E7->Am
notice that it is a 7-cycle of 4ths (except one) starting and ending with minor and all in between by majors but somewhere in the 5th or 6th chord there is shift by a semitone thus not pure 4th.
There are more ways to do so!
E.g.
The relative-chromatic inversion of major-major To inverse the D7-->G we may use the progression G-->Bm-->Bbm-->(Am7)->D7 over the notes d, c#, c. The idea is to start with the G and then pass to its minor upper relative Bm and then by semitone shift to Bbm and one more semitone back to Am , but instead of Am we play D7 which is also a relative also of Am as it has the two common notes a and c !. ( Or to reverse G7-->C, use the sequence C-->Em-->D#m-->(Dm7->)->G7 over the notes g, f#, f)
or C-->Em-->D#m-->Dm7-->D7-->G7
in abstract symbols
to invert 5M7->1M as follows 1M->3m->2#m->2m7->5M7 or
in abstract symbols
to invert 5M7->1M as follows 1M->3m->2#m->2m7->5M7 or
1M->3m->2#m->2m7->2M7-->5M7 or
We discuss in the next some ways to have inversion of resolutions and parallel resolutions.
We have met also the chromatic-chromatic inversion So instead of G->D7, we enhance to G->F#->D#->D7. The idea is to shift by a semitone both chords.
The relative -chromatic inversion of major-minor
E.g. To inverse the B7->Em we go from Em to the major relative G7 then shift chromatically to the F#7 and resolve to B7 so it is the sequence Em->G7->F#7->B7
Reverse of a resolution. This is just the reverse of the resolution , which of course is not a resolution but leads from serenity to anxiety e.g. Em-->B7, Some chord progressions, utilize 1,2, or even 4 Reverses of resolutions and then an final straight resolution which resolves the tension of all the previous reverses of resolutions E.g. C--->G7--->D7--->B7---Em. (We use here the similarity of the sound, because of common notes of the B7 and D7)
Resolutions based on relative chords
Since two relative chords have two notes on common (e.g. Am=(a,c,e), C=(c,e,g)) , if one of the two is one semitone away, then the two chords will have two notes one semitone apart E.g. in the previous example A#m=(a#, c#, e#)-->C, or Abm=(ab, cb, eb)--->C, or C#=(c#,e#, g#)-->Am=(a,c.e). Still another way for the relative chords Am-->C is to change the Am to a major chord A=(a,c#,e)-->C=(c,e,g) that will have one note , in 1-semitone apart.
Relatives-indirect resolution. These resolution are derive from ordinary by substituting the second final chord with its relative. E.g. from the standard resolution to a minor B7-->Em we may derive the relatives-indirect B7-->C or B7-->G resolving to major ,as C and G are major relative chords of Bm. The most common use of such substitutions is to pass from minor chords to relative chords. Of course there is the opposite, where a major is substituted by its relative minor e.g. from the standard resolution D7-->G we may derive the relatives-indirect D7-->Em or D7-->Bm.
The chromatic transition to a relative chord. This is the passage to a relative chord semitone by semitone in other words in a chromatic way. E.g. To go from G to Em (or E) we do the sequence G->Gb->F->E7.
The chromatic transition to a complementary chord
E. to go from A to G, we go A(or Am)->Ab->G. Or to go from
C to D, C->C#->D (Dm)
For example the famous song Dream a little dream of me, has 1) Chromatic-chromatic inversion of a resolution 2) Chromatic transition to a relative chord 3) Chromatic transition to a complementary chord
PAGANINI-LIZT RESOLUTION IN CAMBANELA
In the above famous musical piece we have a persisting pair of chords that comes from that harmonic minor 3M7->6m and this melodic theme at the end of the musical piece resolves not the 6M7->2m as it would be expected but the relative (in F major) of 2m, the Bb , thus 6M7 ->Bb. Similarly if it was 7M7->3m, it would resolve to the 3M7->4M.
Some rules for passing from sadness to joy in the harmony of the chord progressions.
1) Pass and close from minor chords to major chords as relative chords (e.g. as relative chords Em-->C , or Am--A7
2) Or from the triangle minor chords to the triangle of the major chords of the diatonic scale through the diatonic bridge. E.g. Em-->Am-->Dm (Dm7 bridge, or D7) --->G--->C--->G. (1st majorization)
3) Pass from the triangle minor chords to the corresponding same root triangle of major chords
E.g. Em-->Am-->Dm then E7-->A7-->D.(2nd majorization)
4) Use a reverse resolution with minor chord , and then resolve to a straight resolution with major chords E.g. Em-->B7-->D7--G (we use here the similarity of the sound because of common notes of the B7 and D7).
5) Inverse a major-minor resolution (e.g. B7-->Em) to its major chord (here B) by utilizing the major Andalusian cadenza (Em-->D-->C-->B).(3rd majorization)
6) Pass from a resolution of one ot two minor chords e.g. X7-->(x+1), to one with both major chords Y7-->Y+1 E.g. From B7-->Em to D7-->G as in the progression B7-->Em-->C-->D7-->G.
7) Even for sad melodies do not use more than 1/3 of the total number of chord-instances as minor chords. The rest 2/3 should be with major chords. But for highly joyous songs use only major chords and rather few (2-3) than many.
The diatonic progressions is the sequence (iii->vi->ii->V->I->IV->VII->iii), e.g. in C major scale the sequence Em->Am->Dm->G->C->F->Em (Here the symbolism of Roman numerals as it is standard in jazz, it refers to the order of the root of the chord in the scale, and it is capital if it is major and small if it s minor) This progression leads from sadness to joy, from the triad of minor chords to the triad of major chords.
In a diatonic scale, the triad of minor chords (sad triad) is the (iii->vi->ii) where the (iii, vi) and (vi,ii) are consecutive in the cycle of pure 4ths, with standard resolutions (iii7-> vi) , (vi7->ii) and the
(ii, iii) are complementary chords, in other words all of their notes give all the notes of the scale except one.
The triad of joy or triad of major chords is the (V, I, IV) , where the (V, I) and (I,IV) are consecutive in the cycle of pure 4ths, with standard resolutions (V7-> I) , (I7->IV) and the (IV, V) are complementary chords, in other words all of their notes give all the notes of the scale except one.
The bridge between these two triads is the well known jazz progression (ii7, V7, I) , where again the (ii, V) and (V,I) are consecutive in the cycle of pure 4ths, with standard resolutions (ii7-> V) , (V7->I), and the (ii, I) are complementary chords, in other words all of their notes give all the notes of the scale except one.
The diatonic progression closes also to a cycle by utilizing the triad progressions
(IV->IV#7->VII7->iii) or (IV7->VIIb->vi). E.g. in C major scale, F->F#7->B7->Em
Subscribe to:
Comments (Atom)
