When playing melodies in the guitar what matters more is the relative position of notes rather, than the absolute pitch of them. All our western musical system is based on uniformity of translating (transposing) melodies in lower or higher pitch, which makes the distances of the notes a priority in what matters.
We may also classify the intervals to
VERY SMALL in semitones 1, 2 THEY ARE PLAYED IN THE SAME STRING USUALLY
SMALL in semitones 3, 4 THEY ARE PLAYED IN TWO SECLUSIVE STRINGS USUALLY
MEDIUM in semitones 5,6 7 THEY ARE PLAYED IN TWO SECLUSIVE STRINGS USUALLY
BIG in semitones 8,9,10,11, 12 THEY ARE PLAYED USUALLY IN STRINGS, THAT ARE TWO STRINGS APART E.G.6TH- 4TH, 5TH-3RD ETC
VERY BIG in semitones >12 THEY ARE PLAYED USUALLY IN STRINGS, THREE STRINGS APART E.G.6TH-3RD, 5TH-2ND ETC
After the Helmholtz studies (see post 24 ) how good or not good an intervals of notes sounds depends on how many common harmonics they have. The Helmholtz diagram defines also the harmonic hierarchy of the intervals, where the best sounding is of course the unison (0 semitones) distance then the 2nd best is that of the octave (12 semitones) and the 3rd best that of the 5th (7 semitones). These two intervals 0-7-12 define also the R5 chord. The next table gives the harmonic order of the intervals.
Why we have 12 notes in music?
https://www.youtube.com/watch?v=IT9CPoe5LnM&t=409s
Alternative to western system is the chinese musical system
https://simple.wikipedia.org/wiki/Chinese_musical_system
In the Helmholtz just intonation or temperament of intervals (see e.g.
https://en.wikipedia.org/wiki/Just_intonation and
http://www.phy.mtu.edu/~suits/scales.html ), the next small number rational ratios of frequencies correspond to the next musical intervals.
The remarkable book by Helmholtz On the sensation of tone is online here
https://archive.org/details/onsensationsofto00helmrich
In page 193 of the book of Helmholtz is found also the experimental diagram of how the intervals of just temperament sound in dissonance or not in the human ear. The higher the score on the vertical axis the greater the dissonance. The lower end of the horizontal x-axis is the note C, and we see also across the horizontal axis the notes e, f, g, a , b etc.
The smaller a musical interval within an octave the more it signifies sadness, and the more distant, (with maximum a 4th or 5th, as we consider also their inversions) the closer it is to joy.
But the next harmonic score is not about melodies and sadness-joy feelings but more about harmony and stress-serenity feelings.
Interval Bach scale semitones Helmholtz scale rational ratio Harmonic score
Unison (Bach scale 0 semitones) 1 1/1
Octave (12 semitones) 2 1/2
5th perfect (7 semitones) 3/2 1/(3+2)
4th pure (5 semitones) 4/3 1/(4+3)
6th major (9 semitones) 5/3 1/(5+3)
3rd major (4 semitones) 5/4 1/(5+4)
3rd minor (3 semitones) 6/5 1/(6+5)
7th minor (9 semitones) 9/5 1/(9+5)
2nd major (2 semitones) 9/8 1/(9+8)
7th major (10 semitones) 15/18 1/(15+18)
6th minor (8 semitones) 25/16 1/(25+16)
2nd minor (1 semitone) 25/24 (or 9/8) 1/(25+24)
5th diminished (6 semitones) 45/32 1/(45+32)
The smaller the numerator and denominator of the rational ratio of the pitches (in the Helmholts scale) the larger the number of harmonics that are common, when two notes sound with this ratio and thus the better and more harmonic , the interval sounds. In the Bach scale this is a bit ruined but not too much (see also post 24, and if the reader understands Greek also post 25, in the .pdf manuscript page 53).
This harmonic clasification of intervals goes back to ancient Pythagorean ideas, but also to modern discoveries of the nature of senses. For example the flavors and smells are good or bad according to if the "chord" of ultra high frequency sonic high frequencies of its molecules, is harmonic or not . About this see for example the next video.
http://www.ted.com/talks/luca_turin_on_the_science_of_scent
See also about the Pythagorean tuning
https://en.wikipedia.org/wiki/Pythagorean_tuning
Therefore the order of the intervals in the above table is also the order of how good their harmony is when the interval sounds is isolation of anything else.
Notice that the intervals of perfect 4th and 6th sound better than the intervals of 3rd, and the interval of 7th minor better than the interval of 2nd major. The worst of all is the interval of 6 semitone (4th augmented or 5th diminsihed).
Utilizing the harmonic scores in the above table we can define also
harmonic scores of the various chords, by adding the scores of all of their intrevals in all possible ways they shape, divided by the number of these shaped intervals. Let us calculate for example the harmonic scores of the major, minor triads , the R5 chord and the some more chords.
The major triad has intervals M3 m3, P5 , so its harmonic score H(R) is
H(R)=1/3*([1/(5+6)]+[1/(4+5)]+[1/(3+2)])=([1/11]+[1/9]+[1/5])/3=0.134
The harmonic score ofthe minor is the same:
H(Rm)=1/3*([1/(5+6)]+[1/(4+5)]+[1/(3+2)])=([1/11]+[1/9]+[1/5])/3=0.134
Now here one may ask, why then a major triad sounds more harmonious and joyful than a minor triad which sounds more sad? The answer is that the same harmonic score of the minor 3rd interval (3 semitones) sounds less harmonious when it is in lower frequencies, than when it is in higher frequencies. And this explains the different feeling of the major and minor chord, although they have the same harmonic score!
The harmonic score of the R5 chord is the highest:
H(R5)=([1/(3+2)]+[1/(4+3)]+[1/2])/3=0.28
The harmonic score of the R7 is the average of the harmonic scores of it intervals that is
M3, m3, P5, m3, m7, m5
H(M3)=[1/(4+5)]=0.111, H(m3)=([1/(5+6)]=0.090, H(P5)=[1/(3+2)]=0.2, H(m7)=[1/(9+5)]=0.071
H(m5)=[1/(32+45)]=0.012
H(R7)=1/6*([1/(5+6)]+[1/(4+5)]+[1/(3+2)]+[1/(6+5)]+[1/(9+5)]+[1/(45+32)])=0.095
The harmonic score of the Rmaj7 is better than that of R7:
It is the average of the harmonic scores of its intervals M3, m3, P5, M3, P5, M7, and H(M7)=1/(15+18)=0.030
H(Rmaj7)=1/6*([1/(5+6)]+[1/(4+5)]+[1/(3+2)]+[1/(15+18)]+[1/(4+5)]+[1/(3+2)])=0.123
The harmonic score of the Rm7 is less than that of Rmaj7 but greater than tha of R7, and it is the average of the harmonic scores of its intervals M3, m3, P5, m3, P5 , m7,
H(Rm7)=1/6*([1/(5+6)]+[1/(4+5)]+[1/(3+2)]+[1/(3+2)]+[1/(6+5)]+[1/(18+15)])=0.120
The harmonic score of the Rm7b5 is the average of the harmonic scores of its intervals m3, m3, m3,m5, m5, m7,
H(Rm7b5)=1/6*([1/(5+6)]+[1/(6+5)]+[1/(6+5)]+[1/(45+32)]+[1/(9+5)]+[1/(45+32)])=0.06
While the harmonic score of the Rdim7 is slightly better than that of Rm7b5 and it is the average of the harmonic scores of its intervals m3, m3, M2,m5, P4, m6,
H(Rdim7)=1/6*([1/(5+6)]+[1/(6+5)]+[1/(24+25)]+[1/(45+32)]+[1/(16+25)]+[1/(4+3)])=0.063
The harmonic score of the Raug is better than that of Rdim7 ,Rm7b5 and is the average of the harmonic scores of its intervals M3, M3, m6,
H(Raug)=([1/(4+5)]+[1/(4+5)]+[1/(25+16)])/3=0.082
We notice also here that the more notes, a chord has the less would be its harmonic score, compared to chords with few only notes
Therefore the harmonic order of the above chords are
R5>R, Rm>Rmaj7> Rm7>R7>Raug>Rm7b5>Rdim7
We must remark here that these harmonic scores refer to the root position of the chord. The invesrions will have different harmonic score!
The harmonic score of the invesrions of the major and minor triads are the next
H(R, 1st invesion 3-5-1)=1/3*(H(m3)+H(P4)+H(P5))=1/3*([1/(5+6)]+[1/(4+3)]+[1/(3+2)])=0.144
H(R, 2nd invesion 5-1-3)=1/3*(H(M3)+H(P4)+H(P5))=1/3*([1/(4+5)]+[1/(4+3)]+[1/(3+2)])=0.151
In othe words for the major triad , the 2nd invesrion has the highest harmonic score,while the 1st inversion has also higher score than the root position!
H(Rm, 1st invesion 3-5-1)=1/3*(H(M3)+H(P4)+H(P5))=1/3*([1/(5+6)]+[1/(4+3)]+[1/(3+2)])=0.151
H(Rm, 2nd invesion 5-1-3)=1/3*(H(m3)+H(P4)+H(P5))=1/3*([1/(4+5)]+[1/(4+3)]+[1/(3+2)])=0.144
In other words for the minor triad , the 1st inversion has the highest harmonic score,while the 2nd inversion has also higher score than the root position!
We may as well calculate the harmonic score of the moves of a melody, and produce an oscillating diagram of it (
Melody harmonic score oscillator)
Here is a not irrelevant video on microtonal and
polychromatic music
https://www.youtube.com/watch?v=yVKIXCH-5gE
All the intervals, on the guitar fretboard from the root met in the chords R, Rm, R7, Rmaj7, Rm7, Rdim Raug in other words the m2=1,M2=2,m3=3,M3=4,P4=5,P5=7,M6=9,m7=10,M7=11.
Minor 2nd interval=1 semitone
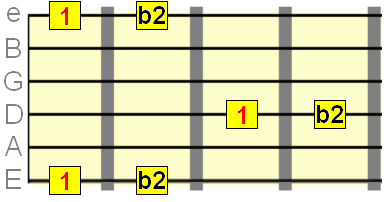
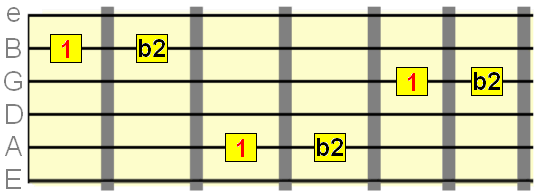
Major 2nd interval=2 semitones
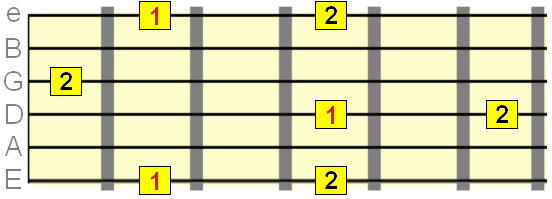
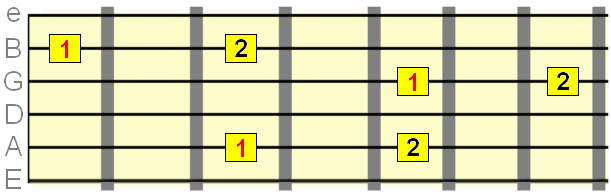
Minor 3rd intevals= 3 semittones
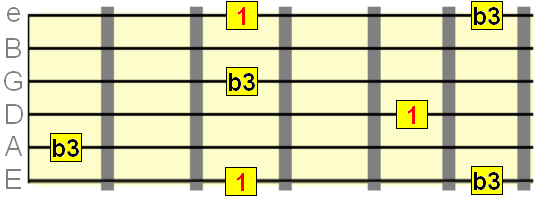
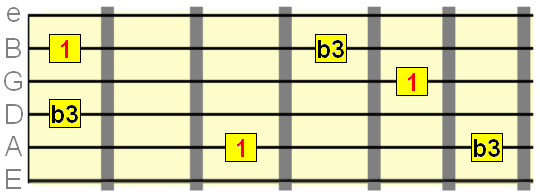
Major 3rd interval= 4 semitones
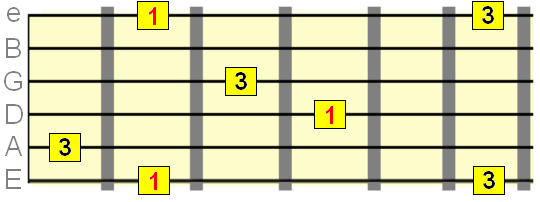
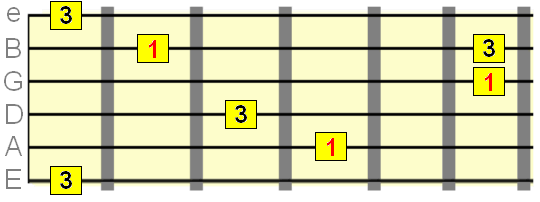
Perfect 4th interval =5 semitones
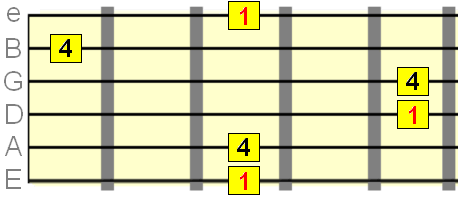
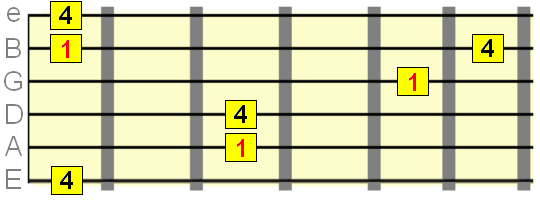
Pute 5th interval=7 semitones
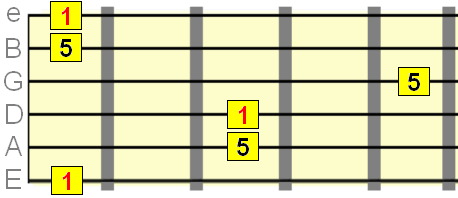
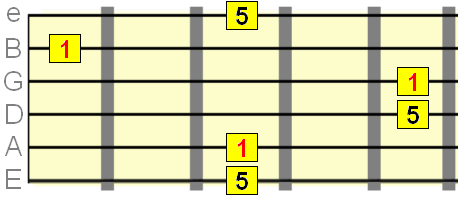
Major 6th interval=9 semitones
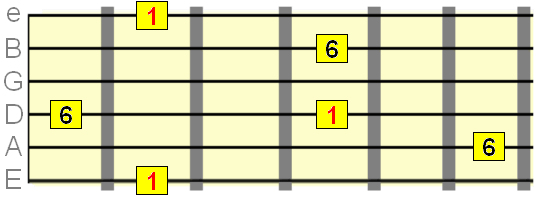
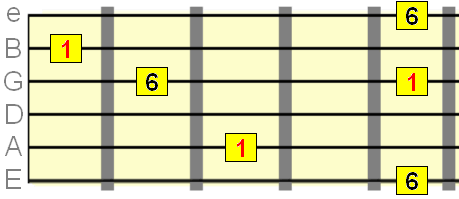
Minor 7th interval=10 semitones
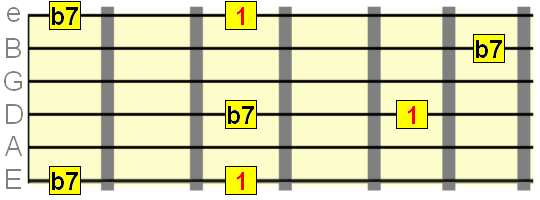
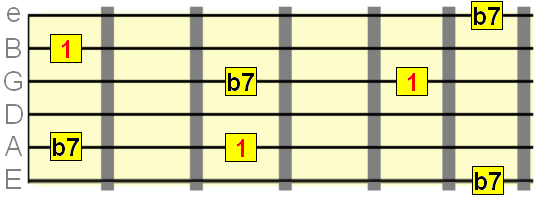
Major 7th interval=11 semitones
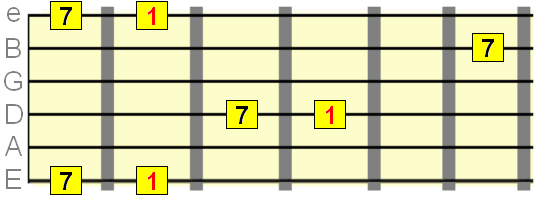
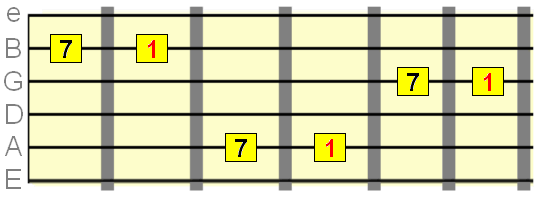
Summarizing with root on the 6th string the M2, M3, P4, P5 ,M6, M7
See also
https://youtu.be/ooPJNYm299k
https://www.youtube.com/watch?v=nmtYaj59slU
http://www.fretjam.com/guitar-intervals-fretboard.html
FOR INTERVAL IMPROVISATION SEE E.G.
https://www.youtube.com/watch?v=binjvIqAN1s
There are of course more types of interval improvisation , that no root is kept always fixed, but the only rule is that at each time an interval sounds rather than only ne note.
A very useful remark for improvisation of melody within a particular chord is the next.
Suppose we are at a note y1 of the melody which fits the underlying chord with notes x1x2x3 (whatever that may mean), then depending on the particular position of y1 relative to the x1x2x3, a shift by an interval of 3rd, 4th, 5th, and 6th wil lead to a note y2 that will again fit the chord!. This is because the relative positions of the notes x1x2x3 of the chord are intervals of major, minor 3rd and pure 5th, and their complementary intervals relative to the octave are minor or major 6th, and pure 4th
SINGING INTERVALS:
https://www.youtube.com/watch?v=Sz-U0X7LBRA




















